
【题目】己知无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,若对于任意的正整数
,若对于任意的正整数![]() ,均有
,均有![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .
.
(1)判断首项为![]() ,公比为
,公比为![]() 的无穷等比数列
的无穷等比数列![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)己知无穷数列![]() 具有性质
具有性质![]() ,且任意相邻四项之和都相等,求证:
,且任意相邻四项之和都相等,求证:![]() ;
;
(3)己知![]() ,数列
,数列![]() 是等差数列,
是等差数列,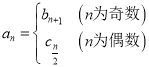 ,若无穷数列
,若无穷数列![]() 具有性质
具有性质![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析(2)证明见解析(3)![]()
【解析】
(1)因为首项为![]() ,公比为
,公比为![]() 的无穷等比数列
的无穷等比数列![]() ,即可
,即可![]() ,求
,求![]() 和
和![]() ,即可求得答案;
,即可求得答案;
(2)因为无穷数列![]() 具有性质
具有性质![]() ,且任意相邻四项之和都相等,
,且任意相邻四项之和都相等,![]() 满足周期性,且
满足周期性,且![]() ,可得
,可得![]() ,因为
,因为![]() 具备性质
具备性质![]() ,故满足:
,故满足:![]() ,
,![]() ,采用反证法证明,即可求得答案;
,采用反证法证明,即可求得答案;
(3)数列![]() 是等差数列,可得
是等差数列,可得![]() 的前
的前![]() 项和为:
项和为:![]() ,因为
,因为![]() 前
前![]() 项和为:
项和为:![]() ,由
,由![]() 具备性质
具备性质![]() ,则
,则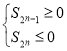 其中
其中![]() 中包含
中包含![]() 项奇数项,
项奇数项,![]() 项偶数项,结合已知,即可求得答案.
项偶数项,结合已知,即可求得答案.
(1)![]() 首项为
首项为![]() ,公比为
,公比为![]() 的无穷等比数列
的无穷等比数列![]()
![]()
![]()
根据等比数列前![]() 项和公式可得:
项和公式可得:
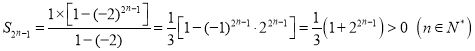 ,
,

![]() 数列
数列![]() 满足具有性质
满足具有性质![]() .
.
(2)![]() 无穷数列
无穷数列![]() 具有性质
具有性质![]() ,且任意相邻四项之和都相等
,且任意相邻四项之和都相等
![]()
![]() 满足周期性,且
满足周期性,且![]()
可得![]()
![]()
![]() 具备性质
具备性质![]()
![]() 满足:
满足:![]() ,
,![]()
利用反正法证明:
若![]() ,则
,则![]() ,
,
令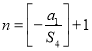
![]() 得:
得:![]() (注:当
(注:当![]() 时,
时,![]() ,则当
,则当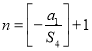 时,
时,![]() )
)
与![]() 矛盾.
矛盾.
![]()
![]() ,
,
又![]()
![]() ,
,
![]()
![]() .证明完毕.
.证明完毕.
(3)![]() 数列
数列![]() 是等差数列
是等差数列
![]()
![]() 的前
的前![]() 项和为:
项和为:![]() ,
,
![]()
![]() 前
前![]() 项和为:
项和为:![]()
由![]() 具备性质
具备性质![]() ,
,
则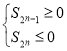
其中![]() 中包含
中包含![]() 项奇数项,
项奇数项,![]() 项偶数项,
项偶数项,
有:![]()
![]()
![]()
其中![]() 中包含
中包含![]() 项奇数项,
项奇数项,![]() 项偶数项,
项偶数项,
故:![]()
![]()
![]()
由性质![]()
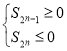
可得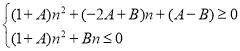 ,对任意
,对任意![]() 成立
成立
![]()
![]() 、
、![]() 满足:
满足: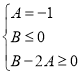 ,解得:
,解得:![]()
![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中,上面7层为高尔顿板,最下面一层为改造的高尔顿板,小球从通道口落下,第一次与第2层中间的小木块碰撞,以![]() 的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以
的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以![]() 的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以
的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以![]() 的概率向右滚下.
的概率向右滚下.

(1)若进行一次高尔顿板试验,求小球落入第7层第6个空隙处的概率;
(2)小明同学在研究了高尔顿板后,利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动,8元可以玩一次高尔顿板游戏,小球掉入X号球槽得到的奖金为![]() 元,其中
元,其中![]() .
.
(i)求X的分布列:
(ii)高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小明同学能盈利吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大学自主招生考生中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生两科的考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有20人.
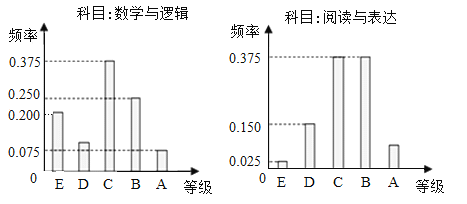
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生“数学与逻辑”科目的平均分;
(ii)若该考场共有7人得分大于7分,其中有2人10分,2人9分,3人8分,从这7中随机抽取两人,求两人成绩之和大于等于18的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:![]() ,当
,当![]() 且
且![]() 时,
时,![]() 且
且![]() ,其中
,其中![]() 均为非零常数.
均为非零常数.
(1)数列![]() 是等差数列,求
是等差数列,求![]() 的值;
的值;
(2)令![]() ,若
,若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)证明:![]() 数列是等比数列的充要条件是
数列是等比数列的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六位同学围成一圈依序循环报数,规定:
①第一位同学首次报出的数为0.第二位同学首次报出的数为1,之后每位同学所报出的数都是前两位同学所报出的数之和:
②若报出的是为3的倍数,则报该数的同学需拍手一次.
当第50个数被报出时,六位同学拍手的总次数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有30位高级教师,其中60%人爱好体育锻炼,经体检调查,得到如下列联表.
身体好 | 身体一般 | 总计 | |
爱好体育锻炼 | 2 | ||
不爱好体育锻炼 | 4 | ||
总计 | 20 |
(1)根据以上信息完成![]() 列联表,并判断有多大把握认为“身体好与爱好体育锻炼有关系”?
列联表,并判断有多大把握认为“身体好与爱好体育锻炼有关系”?
(2)现从身体一般的教师中抽取3人,记3人中爱好体育锻炼的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: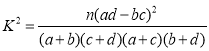 ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①设![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;②若
”的充分不必要条件;②若![]() ,则
,则![]() ,使得
,使得![]() ;③
;③![]() 为等比数列,则“
为等比数列,则“![]() ”是“
”是“![]() ”的充分不必要条件;④命题“
”的充分不必要条件;④命题“![]() ,
,![]() ,使得
,使得![]() ”的否定形式是“
”的否定形式是“![]() ,
,![]() ,使得
,使得![]() ” .其中正确说法的个数为( )
” .其中正确说法的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com