
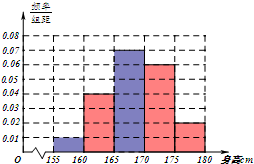
 为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.
为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.| 分组 | 频数 | 频率 |
| [155,160) | ① | 0.050 |
| [160,165) | 20 | 0.200 |
| [165,170) | ② | ③ |
| [170,175) | 30 | 0.300 |
| [175,180) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
| 频率 |
| 组距 |
| ||
|
| 91 |
| 278 |
| ||||
|
| 35 |
| 76 |
| ||||
|
| 5 |
| 38 |
| ||
|
| 1 |
| 114 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 91 |
| 278 |
| 35 |
| 76 |
| 5 |
| 38 |
| 1 |
| 114 |
| 57 |
| 76 |
| 3 |
| 4 |


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:
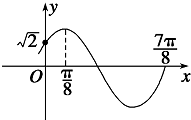 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| f2(x)-2f(x)+2 |
| f(x)-1 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
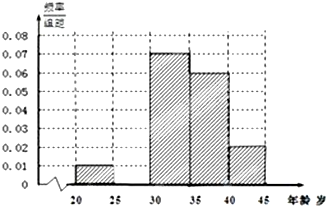 某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| A、an=2n |
| B、an=2n-1 |
| C、an=3n-1 |
| D、an=3n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com