
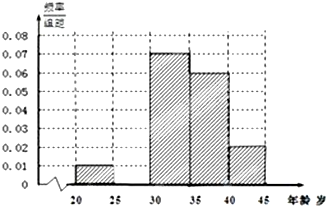
 某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.| 0.2 |
| 5 |


科目:高中数学 来源: 题型:
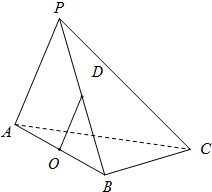 在三棱锥P-ABC中△PAC,△PBC是边长为
在三棱锥P-ABC中△PAC,△PBC是边长为| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.
为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.| 分组 | 频数 | 频率 |
| [155,160) | ① | 0.050 |
| [160,165) | 20 | 0.200 |
| [165,170) | ② | ③ |
| [170,175) | 30 | 0.300 |
| [175,180) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、86.5,1.5 |
| B、86.5,1.2 |
| C、86,1.5 |
| D、86,1.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com