
| A、y=x+1 | ||
B、y=x+
| ||
C、y=x-
| ||
| D、y=x2+1 |
| 1 |
| x |
| 1 |
| x |
| x2-1 |
| x |
| (-x)2-1 |
| -x |
| x2-1 |
| x |
| x2+1 |
| x2 |
| 1 |
| x |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
|
A、(∞,
| ||||
B、[-
| ||||
C、[
| ||||
| D、[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
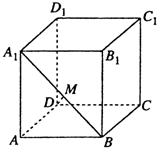 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.查看答案和解析>>
科目:高中数学 来源: 题型:
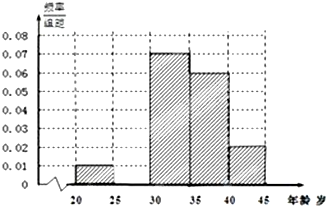 某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| A、命题“?x∈R,ex>0”的否定是“?x∈R,ex<0” |
| B、命题“已知x,y∈R,若x+y≠10”,则x≠5或y≠5是真命题 |
| C、x2+2x≥ax在x∈[0,2]上恒成立?(x2+2x)min≥(ax)min在x∈[0,2]上恒成立” |
| D、命题:若a=-1,则函数f(x)=ax2+2x-1只有一个零点的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com