
分析 (1)由根与系数的关系写出tanA+tanB=8,tanAtanB=4;利用三角形内角和定理与两角和的正切公式计算即可;
(2)由△≥0以及根与系数的关系,求出a≤-4;再利用三角形内角和定理与两角和的正切公式,求出tanC的最小值以及此时对应的tanA、tanB的值.
解答 解:(1)a=8时,x2-8x+4=0,
∴tanA+tanB=8,tanAtanB=4;
∴tanC=tan[π-(A+B)]
=-tan(A+B)
=$\frac{tanA+tanB}{tanAtanB-1}$
=$\frac{8}{3}$:
(2)由题意,△=a2-16≥0,
解得a≥4或a≤-4;
又tanAtanB=4>0,
∴$\left\{\begin{array}{l}{tanA>0}\\{tanB>0}\end{array}\right.$,
∴tanA+tanB=-a>0,
∴a<0,
即a≤-4;
∴tanC=-tan(A+B)=$\frac{tanA+tanB}{tanAtanB-1}$=$\frac{-a}{3}$≥$\frac{4}{3}$,
∴tanC的最小值是$\frac{4}{3}$,此时对应的tanA=tanB=2.
点评 本题考查了根与系数的关系以及三角形内角和定理与两角和的正切公式应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
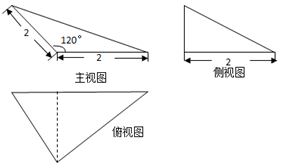
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小说明拟合效果越好 | |
| D. | 若变量y和x之间的相关系数为r=-0.9462,则变量y和x之间具有线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | $x=-\frac{1}{2}$ | C. | x=1 | D. | $x=\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:
某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:| 年份 | 1999 | 2000 | 2001 | 2002 | 2003 |
| 货币收入x | 40 | 42 | 44 | 47 | 50 |
| 购买商品支出y | 33 | 34 | 36 | 39 | 41 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com