
分析 由不等式$\frac{{x}^{2}+1+c}{\sqrt{{x}^{2}+c}}$≥$\frac{1+c}{\sqrt{c}}$(x∈R),可得:$\sqrt{{x}^{2}+c}$+$\frac{1}{\sqrt{{x}^{2}+c}}$≥$\sqrt{c}$+$\frac{1}{\sqrt{c}}$,化为:$(\sqrt{{x}^{2}+c}-\sqrt{c})$$(1-\frac{1}{\sqrt{{x}^{2}+c}•\sqrt{c}})$≥0,由于$\sqrt{{x}^{2}+c}$$-\sqrt{c}$≥0.即有1-$\frac{1}{\sqrt{{x}^{2}+c}•\sqrt{c}}$≥0,可得$\sqrt{{x^2}+c}$•$\sqrt{c}$≥1,化为x2≥$\frac{1}{c}$-c,化为$\frac{1}{c}$-c≤0,即可得出.
解答 解:由不等式$\frac{{x}^{2}+1+c}{\sqrt{{x}^{2}+c}}$≥$\frac{1+c}{\sqrt{c}}$(x∈R),可得:$\sqrt{{x}^{2}+c}$+$\frac{1}{\sqrt{{x}^{2}+c}}$≥$\sqrt{c}$+$\frac{1}{\sqrt{c}}$,
化为:$(\sqrt{{x}^{2}+c}-\sqrt{c})$$(1-\frac{1}{\sqrt{{x}^{2}+c}•\sqrt{c}})$≥0,
由于$\sqrt{{x}^{2}+c}$$-\sqrt{c}$≥0.即有1-$\frac{1}{\sqrt{{x}^{2}+c}•\sqrt{c}}$≥0,可得$\sqrt{{x^2}+c}$•$\sqrt{c}$≥1⇒x2≥$\frac{1}{c}$-c,
若恒成立则必有$\frac{1}{c}$-c≤0,解得$\left\{\begin{array}{l}\frac{{{c^2}-1}}{c}≥0\\ 又c>0\end{array}\right.⇒$c≥1.
故答案为:c≥1.
点评 本题考查了作差法、根式的意义、不等式的解法与性质,考查了推理能力与计算能力,属于中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
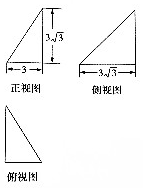 已知某几何体的三视图如图所示,则该几何体的内切球的体积为( )
已知某几何体的三视图如图所示,则该几何体的内切球的体积为( )| A. | $\frac{1}{4}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{1}{2}$π | D. | $\frac{\sqrt{3}}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ea+2a=eb+3b,则a>b | B. | 若ea+2a=eb+3b,则a<b | ||
| C. | 若ea-2a=eb-3b,则a>b | D. | 若ea-2a=eb-3b,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
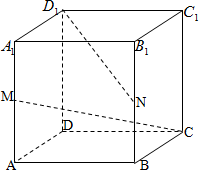 正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:
正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{6}$ | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com