练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．从一堆产品（其中正品与次品都多于2件）中任取2件，观察正品件数和次品件数．则下列事件是互斥事件但不是对立事件的是（　　）
    A．恰好有1件次品和恰好有2件次品B．至少有1件次品和全是次品
    C．至少有1件正品和至少有1件次品D．至少有1件次品和全是正品

    分析 利用对立事件、互斥事件的定义求解．

    解答 解：∵从一堆产品（其中正品与次品都多于2件）中任取2件，观察正品件数和次品件数，
    ∴在A中，恰好有1件次品和恰好有2件次品不能同时发生，但能同时不发生，
    ∴恰好有1件次品和恰好有2件次品是互斥事件但不是对立事件，故A成立；
    在B中，至少有1件次品和全是次品，能同时发生，
    ∴至少有1件次品和全是次品不是互斥事件，故B不成立；
    在C中，至少有1件正品和至少有1件次品能同时发生，
    ∴至少有1件正品和至少有1件次品不是互斥事件，故C不成立；
    在D中，至少有1件次品和全是正品不能同时发生，也不能同时不发生，
    ∴至少有1件次品和全是正品是对立事件，故D不成立．
    故选：A．

    点评 本题考查对立事件、互斥事件的判断，是基础题，解题时要认真审题，注意对立事件、互斥事件的定义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

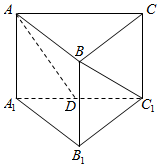    15．已知在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=AA1=2，点D是A1C1的中点，则异面直线AD和BC1所成角的大小为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．定义在R上的偶函数满足f（x+2）=f（x），且在[0，1]上单调递增，设a=f（3），$b=f（\sqrt{2}）$，c=f（2），则a，b，c的大小关系是（　　）
    A．b＞c＞aB．a＞c＞bC．a＞b＞cD．c＞b＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．有一个容量为100的样本，其频率分布直方图如图所示，根据样本的频率分布直方图估计，样本数据落在区间[10，12）内的频数为（　　）
    A．18B．36C．54D．72

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．椭圆C：$\frac{x^2}{4}+\frac{y^2}{3}=1$，过右焦点F且斜率为1的直线L与椭圆C相交于A，B两点
    （1）求右焦点F的坐标
    （2）求弦长AB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知数列{an}满足a1=3，an+1-an=2n，则an=n2-n+3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知抛物线y2=2x，P是抛物线的动弦AB的中点．
    （1）当P的坐标为（2，3）时，求直线AB的方程；
    （2）当直线AB的斜率为1时，求线段AB的垂直平分线在x轴上的截距的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．直线 $\sqrt{3}x+3y+2=0$的倾斜角为（　　）
    A．$\frac{π}{3}$B．$\frac{5π}{6}$C．$\frac{2π}{3}$D．$\frac{π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知椭圆$\frac{x^2}{16}+\frac{y^2}{25}=1$的两个焦点为F1，F2，弦AB过点F1，则△ABF2的周长为（　　）
    A．10B．16C．20D．36

    查看答案和解析>>

    同步练习册答案