
【题目】阅读如图所示的程序框图,输出的结果S的值为( ) 
A.0
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:本框图为“当型“循环结构 当满足n≤2010时,
执行循环体:s=s+sin ![]()
根据s=0,n=1
第1次循环:s=0+sin ![]() =
= ![]()
第2次循环:s= ![]() +
+ ![]() =
= ![]()
第3次循环:s= ![]() +0=
+0= ![]()
第4次循环:s= ![]() +(﹣
+(﹣ ![]() )=
)= ![]()
第5次循环:s= ![]() +2(﹣
+2(﹣ ![]() )=0
)=0
第6次循环:s=0+0=0
第7次循环:s= ![]()
…
当n为6的倍数时,s的值为0
n=2010时,为6的倍数,故此时s=0
n=2011时,s= ![]()
故选B
【考点精析】利用算法的循环结构对题目进行判断即可得到答案,需要熟知在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,循环结构可细分为两类:当型循环结构和直到型循环结构.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了了解某学段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如右图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8. 
(1)将频率当作概率,请估计该学段学生中百米成绩在[16,17)内的人数以及所有抽取学生的百米成绩的中位数(精确到0.01秒);
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市地产数据研究所的数据显示,2016年该市新建住宅销售均价走势如图所示,3月至7月房价上涨过快,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.

(1)地产数据研究所发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试求
之间具有较强的线性相关关系,试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若政府不调控,按照3月份至7月份房价的变化趋势预测12月份该市新建住宅的销售均价.
参考数据:![]() ,
,![]() ,
,![]() ;
;
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且4Sn=(an+1)2(n∈N+). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,证明:
}的前n项和,证明: ![]() ≤Tn<1(n∈N+).
≤Tn<1(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客的购物总额(单位元),将数据按照
位顾客的购物总额(单位元),将数据按照![]()
![]() ,
,![]()
![]() 分成
分成![]() 组,制成了如下图所示的频率分布直方图:
组,制成了如下图所示的频率分布直方图:
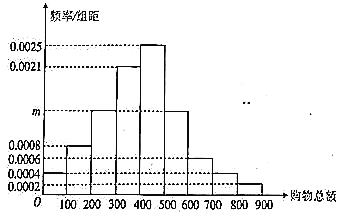
该商场每日大约有![]() 名顾客,为了增加商场销售总额,近期对一次性购物不低于
名顾客,为了增加商场销售总额,近期对一次性购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(1)求频率分布直方图中![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(2)若每日按分层抽样的方法从购物总额在![]() 三组对应的顾客中抽取
三组对应的顾客中抽取![]() 名顾客,这
名顾客,这![]() 名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若 ![]() 且sinC=cosA (Ⅰ)求角A、B、C的大小;
且sinC=cosA (Ⅰ)求角A、B、C的大小;
(Ⅱ)函数f(x)=sin(2x+A)+cos(2x﹣ ![]() ),求函数f(x)单调递增区间,指出它相邻两对称轴间的距离.
),求函数f(x)单调递增区间,指出它相邻两对称轴间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )(x∈R),下面结论错误的是( )
)(x∈R),下面结论错误的是( )
A.函数f(x)的最小正周期为π
B.函数f(x)是偶函数
C.函数f(x)的图象关于直线 ![]() 对称
对称
D.函数f(x)在区间[0, ![]() ]上是增函数
]上是增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像。
的图像。

(1)当![]() 时,若方程
时,若方程![]() 恰好有两个不同的根
恰好有两个不同的根![]() ,求
,求![]() 的取值范围及
的取值范围及![]() 的值;
的值;
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com