
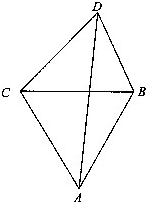
 如图,我军某部军事演习时红方炮兵阵地位于A处,B,C是两雷达观察点,且B位于C正东与C距离为m,已知A与两雷达观察点B,C的距离也均为m,当绿方目标D出现在观察点B的北偏西15°和观察点C的北偏东45°交汇处时及时炮击,求炮击目标的距离AD(A,B,C,D在同一平面(地面)内).
如图,我军某部军事演习时红方炮兵阵地位于A处,B,C是两雷达观察点,且B位于C正东与C距离为m,已知A与两雷达观察点B,C的距离也均为m,当绿方目标D出现在观察点B的北偏西15°和观察点C的北偏东45°交汇处时及时炮击,求炮击目标的距离AD(A,B,C,D在同一平面(地面)内).
| ||
| 3 |
| BC |
| sin∠BDC |
| BD |
| sin∠BCD |
| BC•sin∠BCD |
| sin∠BDC |
| m•sin45° |
| sin60° |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
5-2
| ||
| 3 |
|
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
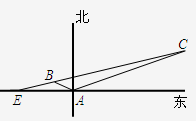 如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.
如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com