
 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.分析 (1)利用二次函数的性质以及函数的奇偶性画出函数的图象,写出单调区间以及函数的值域即可.
(2)利用函数的性质,转化求解函数的解析式即可.
解答 解:(1)图象如图所示: …(3分)
…(3分)
由图象得:函数f(x)的单调递减区间是(-∞,-1)和(0,1);
单调递增区间为(-1,0)和(1,+∞);…(4分)
函数的值域为[-1,+∞).…(5分)
(2)设x<0,则-x>0,
于是,f(-x)=(-x)2-2(-x)=x2+2x.…(7分)
又因为函数f(x)是偶函数,
所以f(x)=f(-x)=x2+2x.…(9分)
所以f(x)的解析式为:$f(x)=\left\{\begin{array}{l}{x^2}-2x\;,\;\;x≥0\;,\;\;\\{x^2}+2x\;,\;\;x<0\;.\;\end{array}\right.$…(10分)
点评 本题考查函数的图象的画法,函数的图象的应用,解析式的求法,考查计算能力.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
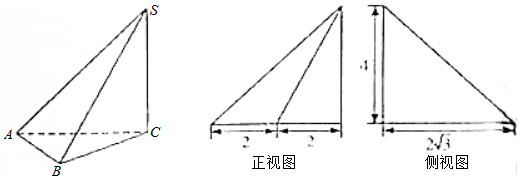
| A. | 32π | B. | $\frac{112π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{64}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{12}$,$\frac{7π}{12}$] | B. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | C. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | D. | [-$\frac{π}{6}$,$\frac{5π}{6}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com