
分析 取MN的中点A,连接OA,则OA⊥MN.由点到直线的距离公式算出OA=1,从而在Rt△AON中,得到cos∠AON=$\frac{1}{4}$,得cos∠MON=-$\frac{7}{8}$,最后根据向量数量积的公式即可算出$\overrightarrow{OM}$•$\overrightarrow{ON}$的值,运用向量的加减运算和向量数量积的定义,可得$\overrightarrow{PM}$•$\overrightarrow{PN}$=2-8cos∠AOP,考虑$\overrightarrow{OP}$,$\overrightarrow{OA}$同向和反向,可得最值,即可得到所求范围.
解答 解:取MN的中点A,连接OA,则OA⊥MN,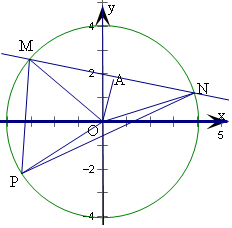
∵c2=a2+b2,
∴O点到直线MN的距离OA=$\frac{|c|}{\sqrt{{a}^{2}+{b}^{2}}}$=1,
x2+y2=16的半径r=4,
∴Rt△AON中,设∠AON=θ,得cosθ=$\frac{OA}{ON}$=$\frac{1}{4}$,
cos∠MON=cos2θ=2cos2θ-1=$\frac{1}{8}$-1=-$\frac{7}{8}$,
由此可得,$\overrightarrow{OM}$•$\overrightarrow{ON}$=|$\overrightarrow{OM}$|•|$\overrightarrow{ON}$|cos∠MON
=4×4×(-$\frac{7}{8}$)=-14,
则$\overrightarrow{PM}$•$\overrightarrow{PN}$=($\overrightarrow{OM}$-$\overrightarrow{OP}$)•($\overrightarrow{ON}$-$\overrightarrow{OP}$)=$\overrightarrow{OM}$•$\overrightarrow{ON}$+$\overrightarrow{OP}$2-$\overrightarrow{OP}$•($\overrightarrow{OM}$+$\overrightarrow{ON}$)
=-14+16-2$\overrightarrow{OP}$•$\overrightarrow{OA}$=2-2|$\overrightarrow{OP}$|•|$\overrightarrow{OA}$|•cos∠AOP=2-8cos∠AOP,
当$\overrightarrow{OP}$,$\overrightarrow{OA}$同向时,取得最小值且为2-8=-6,
当$\overrightarrow{OP}$,$\overrightarrow{OA}$反向时,取得最大值且为2+8=10.
则$\overrightarrow{PM}$•$\overrightarrow{PN}$的取值范围是[-6.10].
故答案为:[-6.10].
点评 本题考查向量的加减运算和向量的数量积的定义,着重考查了直线与圆的位置关系和向量数量积的运算公式等知识点,注意运用转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 20 | C. | 24 | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②①③ | C. | ②③① | D. | ③②① |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
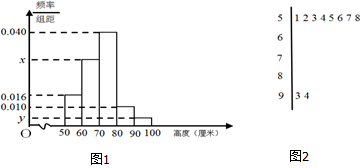
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com