
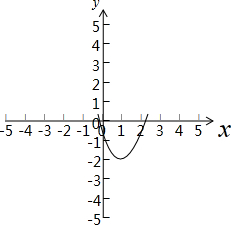 解:∵f(x)=x2-2x-1=(x-1)2-2,∴对称轴x=1,顶点坐标(1,-2),如图所示;
解:∵f(x)=x2-2x-1=(x-1)2-2,∴对称轴x=1,顶点坐标(1,-2),如图所示;
|


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
| x+1-a |
| a-x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图:在直三棱柱ABC-A1B1C1中,AC=BC=C1C,AC⊥CB,D为AB的中点,
如图:在直三棱柱ABC-A1B1C1中,AC=BC=C1C,AC⊥CB,D为AB的中点,查看答案和解析>>
科目:高中数学 来源: 题型:
| 日期编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 空气质量指数(AQI) | 179 | 40 | 98 | 124 | 29 | 133 | 241 | 424 | 95 | 89 |
| “PM2.5”24小时平均浓度(ug/m3) | 135 | 5 | 80 | 94 | 80 | 100 | 190 | 387 | 70 | 66 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com