分析:本题考查的知识点是直线的一般式方程及动点轨迹方程的求法,(1)由于弦AB过点M(1,1),故我们可设出直线AB的点斜式方程,联立直线与圆的方程后,根据韦达定理(根与系数的关系),我们结合点M恰为弦AB的中点,可得到一个关于斜率k的方程,解方程求出k值后,代入整理即可得到直线AB的方程.(2)设AB弦的中点为P,则由A,B,M,P四点共线,易得他们确定直线的斜率相等,由此可构造一个关于x,y的关系式,整理后即可得到过点M的弦的中点的轨迹方程.
解答:解:(1)设直线AB的斜率为k,则AB的方程可设为y-1=k(x-1).
得x
2+4(kx+1-k)
2=16
得(1+4k
2)x
2+8k(1-k)x+4(1-k
2)-16=0
设A(x1,y1),B(x2,y2),则x1+x2=,
而M(1,1)是AB中点,则=1.
综上,得=2,解得k=-.
∴
直线AB的方程为y-1=-(x-1),即x+4y-5=0.
(2)设弦AB的中点为P(x,y)
∵A,B,M,P四点共线,
∴k
AB=k
MP
即(-)•=,而x1+x2=2x,y1+y2=2y∴
(-)=,整理,得轨迹方程为x2+4y2-x-4y=0.
点评:在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件,用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或经过原点的直线,故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.

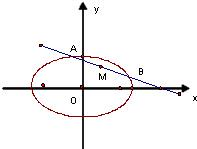 过椭圆
过椭圆

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案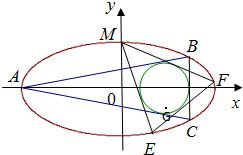 如图,已知圆G:(x-2)2+y2=r2是椭圆
如图,已知圆G:(x-2)2+y2=r2是椭圆