练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知B(－1，1)是椭圆上一点，且点B到椭圆的两个焦点距离之和为4．

    (Ⅰ)求椭圆方程；

    (Ⅱ)设A为椭圆的左顶点，直线AB交y轴于点C，过C作直线l交椭圆于D、E两点，问：是否存在直线l，使得△CBD与△CAE的面积之比为1∶7．若存在，求出直线l的方程；若不存在，说明理由．

    答案：
    解析：

    　　解：(Ⅰ)由已知得：　　1分

    　　　　3分

    　　即椭圆方程为　　4分

    　　(Ⅱ)由、有，∴　　5分

    　　设，，因为不合题意，故可设，

    　　代入　得：　　6分

    　　　　7分

    　　又而，∴

    　　从而　　9分

    　　联立(1)(2)(3)，解得，均满足(*)式的．

    　　即：　　12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f(x)=3sin(2x+
    π
    3
    )    ，则以下不等式正确的是（　　）
    A、f（3）＞f（1）＞f（2）
    B、f（1）＞f（2）＞f（3）
    C、f（3）＞f（2）＞f（1）
    D、f（1）＞f（3）＞f（2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知某海滨浴场的海浪高度y（单位：米）与时间 t（0≤t≤24）（单位：时）的函数关系记作y=f（t），下表是某日各时的浪高数据：
    t/时 0 3 6 9 12 15 18 21 24
    y/米 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
    经长期观测，函数y=f（t）可近似地看成是函数y=Acosωt+b．
    （1）根据以上数据，求出函数y=Acosωt+b的最小正周期T及函数表达 式（其中A＞0，ω＞0）；
    （2）根据规定，当海浪高度不低于0.75米时，才对冲浪爱好者开放，请根据以上结论，判断一天内从上午7时至晚上19时之间，该浴场有多少时间可向冲浪爱好者开放？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

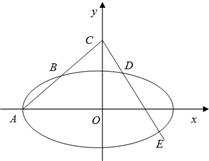    已知B（-1，1）是椭圆
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）上一点，且点B到椭圆的两个焦点距离之和为4；
    （1）求椭圆方程；
    （2）设A为椭圆的左顶点，直线AB交y轴于点C，过C作斜率为k的直线l交椭圆于D，E两点，若
    S△CBD
    S△CAE
    =
    1
    6
    ，求实数k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线
    x2
    a2
    -
    y2
    b2
    =1（b＞a＞0），O为坐标原点，P、Q为双曲线上两动点，且OP⊥OQ．试证明
    （1）
    1
    |OP|2
    +
    1
    |OQ|2
    =
    1
    a2
    -
    1
    b2
    ；
    （2）|OP|2+|OQ|2的最小值为
    4a2b2
    b2-a2
    ；
    （3）S△OPQ的最小值是
    a2b2
    b2-a2
    ．

    查看答案和解析>>

    同步练习册答案