|
|
|
关于x的方程x2+mx+n=0(m,n∈R)的一个根是-3+2i,则m=________.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
设函数f(x)= 为奇函数,则a=________. 为奇函数,则a=________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
已知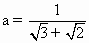 , ,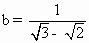 ,则a、b的等差中项是 ,则a、b的等差中项是
|
| [ ] |
A. |

|
B. |
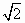
|
C. |
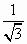
|
D. |
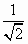
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 平面解析几何
题型:
|
|
|
已知△ABC中,A(4,2),B(1,8),C(-1,8).
(1)求AB边上的高所在的直线方程;
(2)直线l∥AB,与AC,BC依次交于E,F,S△CEF∶S△ABC=1∶4.求l所在的直线方程.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 平面解析几何
题型:
|
|
|
已知曲线C的极坐标方程为ρ=2cos ,则曲线C上的点到直线 ,则曲线C上的点到直线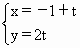 (t为参数)的距离的最大值为________. (t为参数)的距离的最大值为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
若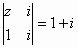 (i为虚数单位),则z=________. (i为虚数单位),则z=________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
设等差数列{an}的前n项和为Sn,且a5+a13=34,S3=9.数列{bn}的前n项和为Tn,满足Tn=1-bn.
(1)求数列{an}的通项公式;
(2)写出一个正整数m,使得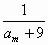 是数列{bn}的项; 是数列{bn}的项;
(3)设数列{cn}的通项公式为 ,问:是否存在正整数t和k(k≥3),使得c1,c2,ck成等差数列?若存在,请求出所有符合条件的有序整数对(t,k);若不存在,请说明理由. ,问:是否存在正整数t和k(k≥3),使得c1,c2,ck成等差数列?若存在,请求出所有符合条件的有序整数对(t,k);若不存在,请说明理由.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知公差为-2的等差数列{an}的前n项和为Sn,且a1=7,则使Sn<0成立的最小的自然数n的值为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修5
题型:
|
|
|
在平面直角坐标系内,设M(x1,y1)、N(x2,y2)为不同的两点,直线l的方程为ax+by+c=0,△1=ax1+by1+c,△2=ax2+by2+c.有四个命题:
①若△1△2>0,则点M、N一定在直线l的同侧;
②若△1△2<0,则点M、N一定在直线l的两侧;
③若△1+△2=0,则点M、N一定在直线l的两侧;
④若 ,则点M到直线l的距离大于点N到直线l的距离. ,则点M到直线l的距离大于点N到直线l的距离.
上述命题中,全部真命题的序号是
|
| [ ] |
A. |
①②③
|
B. |
①②④
|
C. |
②③④
|
D. |
①②③④
|
|
|
查看答案和解析>>
