


科目:高中数学 来源: 题型:解答题
 )=0,求f(x)的单调区间;
)=0,求f(x)的单调区间;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 的大小关系.
的大小关系.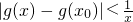 对任意x>0成立?若存在,求出x0的取值范围,若不存在,请说明理由.
对任意x>0成立?若存在,求出x0的取值范围,若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
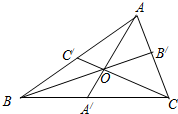 已知O是△ABC内任意一点,连接AO,BO,CO并延长交对边于A′,B′,C′,则
已知O是△ABC内任意一点,连接AO,BO,CO并延长交对边于A′,B′,C′,则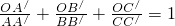 ,这是平面几何中的一个命题,其证明方法常采用“面积法”:
,这是平面几何中的一个命题,其证明方法常采用“面积法”: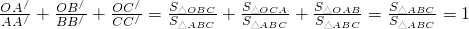 .运用类比猜想,对于空间四面体存在什么类似的命题?并用“体积法”证明.
.运用类比猜想,对于空间四面体存在什么类似的命题?并用“体积法”证明.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
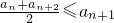 ; ②an≤M.其中n∈N*,M是与n无关的常数.
; ②an≤M.其中n∈N*,M是与n无关的常数.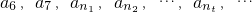 成等比数列. 若bm=10m-nm(m∈N*),则{bm}∈A是否成立?若成立,求M的取值范围,若不成立,请说明理由;
成等比数列. 若bm=10m-nm(m∈N*),则{bm}∈A是否成立?若成立,求M的取值范围,若不成立,请说明理由;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com