
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,且
为菱形,且![]() ,
,![]() 是边长为
是边长为![]() 的正三角形,且平面
的正三角形,且平面![]() 平面
平面![]() ,已知点
,已知点![]() 是
是![]() 的中点.
的中点.
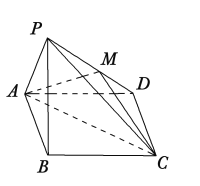
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,由中位线定理可得
,由中位线定理可得![]() ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得![]() 平面
平面![]() ;(2)取
;(2)取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() 平面
平面![]() ,由
,由![]() ,即可求出三棱锥
,即可求出三棱锥![]() 的体积.
的体积.
试题解析:(Ⅰ)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,
因为![]() 为菱形,
为菱形,![]() ,所以
,所以![]() ,
,
由直线![]() 不在平面
不在平面![]() 内,
内,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() .
.
因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() ,
,
又![]() 是
是![]() 中点,所以
中点,所以![]() .
.
所以![]()
![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、面面垂直的性质、线面垂直的判定、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:

该省某市2016年11月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(附参考公式: ![]() ,其中
,其中 ,
, ![]() )
)
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数由相关关系,如表3:
指数由相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: 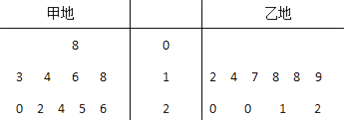
规定:当产品中的此种元素含量≥15毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
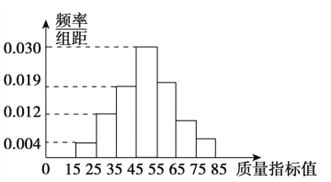
【题目】质检部门从企业生产的产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
(Ⅰ)求这些产品质量指标值落在区间![]() 内的频率;
内的频率;
(Ⅱ)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间![]() 内的产品件数为
内的产品件数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,D、F分别是BC、AC的中点, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)用 ![]() 、
、 ![]() 表示向量
表示向量 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;
;
(2)求证:B、E、F三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若关于x的方程f(f(x))=0有且只有一个实数解,则实数a的取值范围是( )
,若关于x的方程f(f(x))=0有且只有一个实数解,则实数a的取值范围是( )
A.(﹣∞,0)
B.(﹣∞,0]∪(0,1)
C.(﹣∞,0)∪(0,1]
D.(﹣∞,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的个数是( )
)(x∈(0,1))其中成立的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的图象过点(0,﹣1).
的图象过点(0,﹣1).
(1)求实数a的值;
(2)若f(x)=m+ ![]() (m,n是常数),求实数m,n的值;
(m,n是常数),求实数m,n的值;
(3)用定义法证明:函数f(x)在(3,+∞)上是单调减函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com