
| A. | [-1,2] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪(2,+∞) | D. | (-∞,-1)∪[2,+∞) |
分析 求得f(x)的导数,可得切线l1的斜率k1,求得g(x)的导数,可得切线l2的斜率k2,运用两直线垂直的条件:斜率之积为-1,结合正弦函数的值域和条件可得(-1,0)⊆[2-|a|,2+|a|],得到不等式组,解得a的范围即可.
解答 解:∵函数f(x)=lnx+x,∴f′(x)=$\frac{1}{x}+1$,x>0,
∴过函数f(x)=lnx+x的图象上任意一点处的切线l1的斜率k1=$\frac{1}{{x}_{1}}+1$,
∵g(x)=2x+acosx,∴g′(x)=2-asinx,
∵过函数f(x)=lnx+x的图象上任意一点处的切线为l1,
总存在过函数g(x)=2x+acosx的图象上一点处的切线l2,
∴切线l2的斜率k2=2-asinx2,
∵l1⊥l2,∴k1k2=($\frac{1}{{x}_{1}}$+1)(2-asinx2)=-1,
∴2-asinx2=-$\frac{{x}_{1}}{{x}_{1}+1}$=-1+$\frac{1}{{x}_{1}+1}$,
∵x1>0,∴-$\frac{{x}_{1}}{{x}_{1}+1}$∈(-1,0),
2-asinx2∈[2-|a|,2+|a|],
∵?x1,?x2使得等式成立,
∴(-1,0)⊆[2-|a|,2+|a|],
∴$\left\{\begin{array}{l}{2-|a|≤-1}\\{2+|a|≥0}\end{array}\right.$,故|a|≥3,
解得:a≥3或a≤-3,
故选:B.
点评 本题考查导数的应用:求切线的斜率,考查两直线垂直的条件:斜率之积为-1,以及转化思想的运用,区间的包含关系,考查运算能力,属于中档题.


科目:高中数学 来源:2016-2017学年重庆市高一上学期第一次月考数学试卷(解析版) 题型:选择题
下调查方式中,不合适的是( )
A.浙江卫视“奔跑吧兄弟”综艺节目的收视率,采用抽查的方式
B.了解某渔场中青鱼的平均重量,采用抽查的方式
C.了解iphone6s手机的使用寿命,采用普查的方式
D.了解一批汽车的刹车性能,采用普查的方式
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
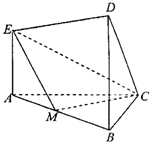 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -2 | C. | 2 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({2x+\frac{π}{3}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({2x-\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com