
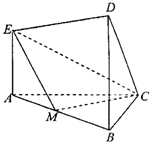
 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.分析 (Ⅰ)由EA⊥平面ABC,结合线面垂直的判定可得平面EAM⊥平面ABC,由已知可得CM⊥AB,再由线面垂直的性质得到CM⊥平面CAM,进一步得到CM⊥EM;
(Ⅱ)由EA⊥平面ABC,DB⊥平面ABC,可得四边形ABDE为直角梯形,由(Ⅰ)知CM⊥平面ABDE,再由棱锥体积公式求得多面体ABCDE的体积;
(Ⅲ)连结MD,解三角形可得DM⊥EM.再由CM⊥平面EMD得CM⊥DM,则DM⊥平面EMC,可得∠DEM是直线DE和平面EMC所成的角,则其正切值可求.
解答 (Ⅰ)证明:∵EA⊥平面ABC,EA?平面EAM,
∴平面EAM⊥平面ABC,且平面EAM∩平面ABCAB.
∵AC=BC,M是AB的中点, ∴CM⊥AB,
∴CM⊥AB,
则CM⊥平面CAM,
∴CM⊥EM;
(Ⅱ)解:∵EA⊥平面ABC,DB⊥平面ABC,
∴四边形ABDE为平面图形,且为直角梯形,
由(Ⅰ)知CM⊥平面ABDE,
∵AC=BC=BD=2AE=2,
∴多面体ABCDE的体积V=VC-ABDE=$\frac{1}{3}×\frac{1}{2}(1+2)×2\sqrt{2}×\sqrt{2}=2$;
(Ⅲ)解:连结MD,∵AC=BC=BD=2AE=2,
在直角梯形EABD中,AB=$2\sqrt{2}$,M是AB的中点.
∴EM=$\sqrt{3}$,MD=$\sqrt{6}$,DE=3,
由EM2+MD2=DE2,得DM⊥EM.
∵CM⊥平面EMD,∴CM⊥DM,得DM⊥平面EMC,
∴∠DEM是直线DE和平面EMC所成的角.
在Rt△EMD中,tan∠DEM=$\frac{MD}{EM}=\sqrt{2}$.
∴直线DE与平面EMC所成的角的正切值为$\sqrt{2}$.
点评 本题考查空间中直线与直线的位置关系,考查多面体体积的求法,训练了线面角的求法,属中档题.


科目:高中数学 来源:2016-2017学年重庆市高一上学期第一次月考数学试卷(解析版) 题型:解答题
重庆某重点中学高一新生小王家在县城A地,现在主城B地上学。周六小王的父母从早上8点从家出发,驾车3小时到达主城B地,期间由于交通等原因,小王父母的车所走的路程 (单位:km)与离家的时间
(单位:km)与离家的时间 (单位:h)的函数关系为
(单位:h)的函数关系为 。达到主城B地后,小王父母把车停在B地,在学校陪小王玩到16点,然后开车从B地以
。达到主城B地后,小王父母把车停在B地,在学校陪小王玩到16点,然后开车从B地以 的速度沿原路返回。
的速度沿原路返回。
(1)求这天小王父母的车所走路程 (单位:km)与离家时间
(单位:km)与离家时间 (单位:h)的函数解析式;
(单位:h)的函数解析式;
(2)在距离小王家60 处有一加油站,求这天小王父母的车途经加油站的时间。
处有一加油站,求这天小王父母的车途经加油站的时间。
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪(2,+∞) | D. | (-∞,-1)∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 750 | B. | 450 | C. | 300 | D. | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,已知某几何体的三视图,则该几何体的体积是1,表面积为$\frac{7}{2}+\frac{3\sqrt{5}}{2}+\sqrt{2}$.
如图所示,已知某几何体的三视图,则该几何体的体积是1,表面积为$\frac{7}{2}+\frac{3\sqrt{5}}{2}+\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com