练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．海面上有A，B，C三个灯塔，AB=10nmile，$BC=5\sqrt{6}$nmile，从A望C和B成600视角，则从B望C和A成（　　）视角．
    A．750B．450C．300D．150

    分析 由题意抽象出△ABC，然后利用正弦定理求解．

    解答 解：如图，

    AB=10，BC=$5\sqrt{6}$，∠BAC=60°．
    由正弦定理可得：$\frac{10}{sinC}=\frac{5\sqrt{6}}{sin60°}=\frac{5\sqrt{6}}{\frac{\sqrt{3}}{2}}=10\sqrt{2}$，
    ∴sinC=$\frac{\sqrt{2}}{2}$，
    ∵10$＜5\sqrt{6}$，∴C=45°．
    则∠ABC=180°-60°-45°=75°．
    故从B望C和A成75°视角．
    故选：A．

    点评 本题考查了正弦定理在实际问题中的应用，理解题意，建立关系是解题的关键．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016-2017学年河南八市高二文上月考一数学试卷（解析版） 题型：选择题

    在中，内角，，所对的边分别是，，，已知，，则（ ）

    A． B．

    C. D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

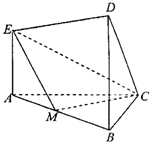    9．在如图所示的几何体中．EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE=2，M是AB的中点．
    （Ⅰ）求证：CM⊥EM；
    （Ⅱ）求多面体ABCDE的体积
    （Ⅲ）求直线DE与平面EMC所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知向量$\overrightarrow{α}$，$\overrightarrow{β}$，$\overrightarrow{γ}$ 满足|$\overrightarrow{α}$|=1，$\overrightarrow{α}$⊥（$\overrightarrow{α}$-2$\overrightarrow{β}$），（$\overrightarrow{α}$-$\overrightarrow{γ}$）⊥（$\overrightarrow{β}$-$\overrightarrow{γ}$），若|$\overrightarrow{β}$|=$\frac{\sqrt{17}}{2}$，|$\overrightarrow{γ}$|的最大值和最小值分别为m，n，则m+n等于（　　）
    A．$\frac{3}{2}$B．2C．$\frac{5}{2}$D．$\frac{{\sqrt{15}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若函数y=f（x）同时具有下列三个性质：（1）最小正周期为π；（2）在$x=\frac{π}{3}$时取得最大值1；（3）在区间$[{-\frac{π}{6}，\frac{π}{3}}]$上是增函数．则y=f（x）的解析式可以是（　　）
    A．$y=sin（{\frac{x}{2}+\frac{π}{6}}）$B．$y=cos（{2x+\frac{π}{3}}）$C．$y=sin（{2x-\frac{π}{6}}）$D．$y=cos（{2x-\frac{π}{6}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知e是自然对数的底数，f（x）=mex，g（x）=x+3，φ（x）=f（x）+g（x），h（x）=f（x）-g（x-2）-2017．
    （Ⅰ）设m=1，求h（x）的极值；
    （Ⅱ）设m＜-e2，求证：函数φ（x）没有零点；
    （Ⅲ）若m≠0，设$F（x）=\frac{m}{f（x）}+\frac{4x+4}{\begin{array}{l}g（x）-1\end{array}}$，求证：F（x）＞3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0，且0≤α＜β＜γ＜2π，则β-α=（　　）
    A．$\frac{4π}{3}或\frac{2π}{3}$B．$\frac{2π}{3}$C．$\frac{4π}{3}$D．以上答案都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．用身高x（cm）预报体重$\stackrel{∧}{y}$（kg）满足$\stackrel{∧}{y}$=0.849x-85.712，若要找到41.638kg的人，不一定是在身高为150cm的人中（填“一定”、“不一定”）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知向量$\overrightarrow{a}$=（sinx，1），$\overrightarrow{b}$=（2cosx，3），x∈R．
    （1）当$\overrightarrow{b}$=λ$\overrightarrow{a}$时，求实数λ和tanx的值；
    （2）设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，求f（x）的最小正周期和单调递减区间．

    查看答案和解析>>

    同步练习册答案