Question

6．已知向量$\overrightarrow{α}$，$\overrightarrow{β}$，$\overrightarrow{γ}$ 满足|$\overrightarrow{α}$|=1，$\overrightarrow{α}$⊥（$\overrightarrow{α}$-2$\overrightarrow{β}$），（$\overrightarrow{α}$-$\overrightarrow{γ}$）⊥（$\overrightarrow{β}$-$\overrightarrow{γ}$），若|$\overrightarrow{β}$|=$\frac{\sqrt{17}}{2}$，|$\overrightarrow{γ}$|的最大值和最小值分别为m，n，则m+n等于（　　）

• A． $\frac{3}{2}$
• B． 2
• C． $\frac{5}{2}$
• D． $\frac{{\sqrt{15}}}{2}$

Answer 1

分析 把$\overrightarrow{α}$放入平面直角坐标系中，使$\overrightarrow{α}$起点与坐标原点重合，方向与x轴正方向一致，得$\overrightarrow{α}$=（1，0）；设$\overrightarrow{β}$=（x₁，y₁），求出$\overrightarrow{β}$的坐标表示，再设$\overrightarrow{γ}$=（x，y），利用坐标表示（$\overrightarrow{α}$-$\overrightarrow{γ}$）•（$\overrightarrow{β}$-$\overrightarrow{γ}$）=0，求出点（x，y）表示的几何图形，利用数形结合求出|$\overrightarrow{γ}$|=$\sqrt{{x}^{2}{+y}^{2}}$的最大值m和最小值n，求和即可．

解答 解：向量$\overrightarrow{α}$，$\overrightarrow{β}$，$\overrightarrow{γ}$ 满足|$\overrightarrow{α}$|=1，$\overrightarrow{α}$⊥（$\overrightarrow{α}$-2$\overrightarrow{β}$），
∴$\overrightarrow{α}$•（$\overrightarrow{α}$-2$\overrightarrow{β}$）=${\overrightarrow{α}}^{2}$-2$\overrightarrow{α}$•$\overrightarrow{β}$=1-2$\overrightarrow{α}$•$\overrightarrow{β}$=0，
∴$\overrightarrow{α}$•$\overrightarrow{β}$=$\frac{1}{2}$；
把$\overrightarrow{α}$放入平面直角坐标系，使$\overrightarrow{α}$起点与坐标原点重合，方向与x轴正方向一致，
则$\overrightarrow{α}$=（1，0）；
设$\overrightarrow{β}$=（x₁，y₁），则$\overrightarrow{α}$•$\overrightarrow{β}$=x₁=$\frac{1}{2}$，
且|$\overrightarrow{β}$|=$\sqrt{{{x}_{1}}^{2}{{+y}_{1}}^{2}}$=$\sqrt{\frac{1}{4}{{+y}_{1}}^{2}}$=$\frac{\sqrt{17}}{2}$，
∴y₁=±2，不妨取$\overrightarrow{β}$=（$\frac{1}{2}$，2）；
设$\overrightarrow{γ}$=（x，y），则$\overrightarrow{α}$-$\overrightarrow{γ}$=（1-x，-y），$\overrightarrow{β}$-$\overrightarrow{γ}$=（$\frac{1}{2}$-x，2-y），
由题意（$\overrightarrow{α}$-$\overrightarrow{γ}$）•（$\overrightarrow{β}$-$\overrightarrow{γ}$）=0，
∴（1-x）（$\frac{1}{2}$-x）-y（2-y）=0，
化简得，x²+y²-$\frac{3}{2}$x-2y+$\frac{1}{2}$=0，即${（x-\frac{3}{4}）}^{2}$+（y-1）²=$\frac{17}{16}$，
则点（x，y）表示圆心在（$\frac{3}{4}$，1），半径为$\frac{\sqrt{17}}{4}$的圆上的点，
如图所示，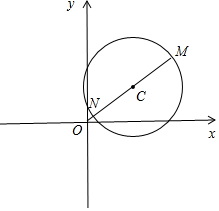

则|$\overrightarrow{γ}$|=$\sqrt{{x}^{2}{+y}^{2}}$的最大值为m=|OC|+r=$\sqrt{{（\frac{3}{4}）}^{2}{+1}^{2}}$+$\frac{\sqrt{17}}{4}$=$\frac{5}{4}$+$\frac{\sqrt{17}}{4}$，
最小值为n=|OC|-r=$\sqrt{{（\frac{3}{4}）}^{2}{+1}^{2}}$-$\frac{\sqrt{17}}{4}$=$\frac{5}{4}$-$\frac{\sqrt{17}}{4}$；
∴m+n=$\frac{5}{2}$．
故选：C．

点评 本题考查了平面向量的坐标运算问题，也考查了数形结合的解法方法，是较难的题目．