
分析 先由:2α+β=π,结合配方法将y=cos(π-2α)-6siα转化为:y=2(sinα-$\frac{3}{2}$)2-$\frac{11}{2}$,再令t=sinα∈(0,1),用二次函数的性质求解.
解答 解:∵一个三角形两内角α、β满足2α+β=π,∴α、β均大于零,∴2α<π,∴α∈(0,$\frac{π}{2}$).
则y=cosβ-6sinα=cos(π-2α)-6sinα
=-cos2α-6sinα=2sin2α-6sinα-1=2(sinα-$\frac{3}{2}$)2-$\frac{11}{2}$,
令t=sinα,根据α∈(0,$\frac{π}{2}$),可得t∈(0,1),则y=2${(t-\frac{3}{2})}^{2}$-$\frac{11}{2}$,
∴当t=0时,y=-1;当t=1时,y=-5,且函数y在(0,1)上单调递减,
∴y∈(-5,-1),
故答案为:(-5,-1).
点评 本题主要考查角的变换及倍角公式在转化函数中的应用,一般来讲考查函数的性质时要转化为基本函数求解,要特别注意α的范围,这是解题的易错点,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2016-2017学年重庆市高一上学期第一次月考数学试卷(解析版) 题型:填空题
从-1,0,1,3,4,这五个数中任选一个数记为a,则使双曲线 在第一、三象限且不等式组
在第一、三象限且不等式组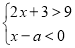 无解的概率是 .
无解的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
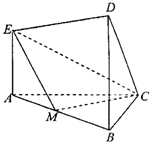 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第8项 | B. | 第9项 | C. | 第10项 | D. | 第11项 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{15}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com