
���� ����1����9��t��17ʱ��$f��t��=1000cos\frac{��t-9����}{4}+2000$����t=13ʱ��f��t��min=1000����-1��+2000=1000����2����0��t��9��17��t��24ʱ��f��t��=3000��
�Ӷ�����Сֵ����Ӧ��ʱ�䣻
���ⷨ1������f��t��=2000ʱ��$cos\frac{��t-9����}{4}=0$���Ӷ��ɵ�t=11��t=15���Ӷ���ã�
�ⷨ2����f��t����2000��$1000cos\frac{��t-9����}{4}+2000��2000$���Ӷ����11��t��15���Ӷ���ã�
��� �⣺����1����9��t��17ʱ��$f��t��=1000cos\frac{��t-9����}{4}+2000$��
��$0��\frac{��t-9����}{4}��2��$��
��$��\frac{��t-9����}{4}=�У�\;\;��t=13ʱ��cos\frac{��t-9����}{4}=-1$��
f��t��min=1000����-1��+2000=1000��
��2����0��t��9��17��t��24ʱ��f��t��=3000��
���ԣ�һ���и��������ܶȵ���Сֵ��1000��ֻ/�����ף���������Сֵʱ��ʱ��t=13��
���ⷨ1�������f��t����2000ʱ���ɱ������ܸ����������������ţ�
��f��t��=2000����$cos\frac{��t-9����}{4}=0$��
�ߵ�9��t��17ʱ��$0��\frac{��t-9����}{4}��2��$��
��$\frac{��t-9����}{4}=\frac{��}{2}$��$\frac{��t-9����}{4}=\frac{3��}{2}$��
��t=11��t=15��
������11������Ͽ�ȿɱ������ܸ����������������ţ�
���ⷨ2�������⣬��f��t����2000ʱ���ɱ������ܸ����������������ţ�
��f��t����2000����$1000cos\frac{��t-9����}{4}+2000��2000$����$cos\frac{��t-9����}{4}��0$��
��$2k��+\frac{��}{2}��\frac{��t-9����}{4}��2k��+\frac{3��}{2}��k��Z$��
�� 8k+11��t��8k+15��k��Z��
�֡�9��t��17��
��11��t��15��
������11������Ͽ�ȿɱ������ܸ����������������ţ�
���� ���⿼���˷ֶκ�����ʵ�������е�Ӧ�ã�ͬʱ���������Ǻ�����Ӧ�ã������е��⣮


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������ | ������F�� | ��������V�� | ������E�� |
| ���� | 5 | 6 | 9 |
| ���� | 6 | 6 | 10 |
| ������] | 6 | 8 | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 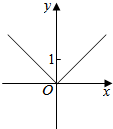 | ||
| C�� |  | D�� | 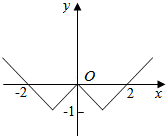 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com