
| 3 |
| 5 |
| 4 |
| 5 |
| sin2α+cos2α+1 |
| 1+tanα |
| π |
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
| 24 |
| 25 |
| 7 |
| 25 |
| sin2α+cos2α+1 |
| 1+tanα |
-
| ||||
1+(-
|
| 18 |
| 25 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 7 |
| 25 |


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
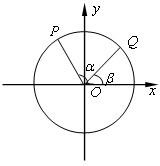
 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为(-
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为(-| 3 |
| 5 |
| 4 |
| 5 |
| sin2α+cos2α+1 |
| 1+tanα |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
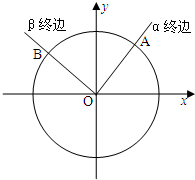
| A、sin(α+β) |
| B、sin(α-β) |
| C、cos(α+β) |
| D、cos(α-β) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 3 |
| 5 |
| 4 |
| 5 |
| sin2α+cos2α+1 |
| 1+tanα |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源:2013年江苏省盐城市滨海县八滩中学高考数学模拟试卷(解析版) 题型:解答题
 .
. 的值;
的值; ,求sin(α+β).
,求sin(α+β).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com