
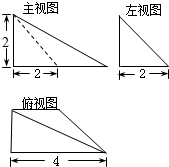
 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )| A、2 | B、4 | C、6 | D、12 |
 解:如图三视图复原的几何体是底面为直角梯形的四棱锥,
解:如图三视图复原的几何体是底面为直角梯形的四棱锥,| 1 |
| 3 |
| AD+BC |
| 2 |
| 1 |
| 3 |
| 2+4 |
| 2 |


科目:高中数学 来源: 题型:
| 2 | 7 | 12 | 17 | 22 | … |
| … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:
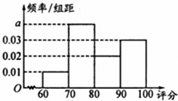 为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.
为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2(Sn-n) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com