
【题目】(选修4—5:不等式选讲)
已知函数![]() .
.
(1)若不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的值;
的值;
(2)若对![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据绝对值定义,将不等式转化为三个不等式组,根据不等式![]() 的解集得形式,只需讨论两种:当
的解集得形式,只需讨论两种:当![]() ,即
,即![]() ,得
,得![]() ,当
,当![]() ,即
,即![]() ,因此
,因此![]() 解得
解得![]() (2)根据绝对值定义,将不等式转化为三个不等式组,当
(2)根据绝对值定义,将不等式转化为三个不等式组,当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ;当
;当![]() ,
,![]() ;再根据三种情况下不等式恒成立关系,转化对应函数最值
;再根据三种情况下不等式恒成立关系,转化对应函数最值![]() ;
;![]() ;
;![]() ,最后求它们的交集得
,最后求它们的交集得![]()
试题解析:(1)![]() ,
,
法一:由已知得 ,.......................2分
,.......................2分
当![]() ,即
,即![]() ,得
,得![]() ;.....................3分
;.....................3分
当![]() ,即
,即![]() ,.........................4分
,.........................4分
由已知![]() 的解集为
的解集为![]() 或,则显然
或,则显然![]() .................5分
.................5分
法二:由已知易得![]() 的图象关于直线
的图象关于直线![]() 对称,..............3分
对称,..............3分
又![]() 的解集为
的解集为![]() ,则
,则![]() ,即
,即![]() ........5分
........5分
(2)法一:不等式![]() 恒成立,即
恒成立,即![]() 恒成立................6分
恒成立................6分
当![]() 时,即
时,即![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() ;................... 7分
;................... 7分
当![]() ,即
,即![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() ;............8分
;............8分
当![]() ,即
,即![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() ............ 9分
............ 9分
综上得![]() .................10分
.................10分
法二:不等式![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
由图象可知![]() 在
在![]() 处取得最小值
处取得最小值![]() ,..............8分
,..............8分
而![]() 在
在![]() 处取得最大值,故
处取得最大值,故![]() ,得
,得![]() ..............10分
..............10分


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(1)已知产量![]() 和能耗
和能耗![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: 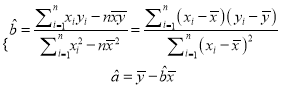
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长为![]() 的直四棱柱
的直四棱柱![]() 中,底面
中,底面![]() 为棱形,
为棱形, ![]() 为棱
为棱![]() 上一点,且
上一点,且![]()

(1)求证:平面![]() 平面
平面![]() ;
;
(2)平面![]() 将四棱柱
将四棱柱![]() 分成上、下两部分,求这两部分的体积之比.
分成上、下两部分,求这两部分的体积之比.
(棱台的体积公式为![]() ,其中
,其中![]() 分别为上、下底面面积,
分别为上、下底面面积, ![]() 为棱台的高)
为棱台的高)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() +
+![]() =1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
=1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
(1)求椭圆E的方程;
(2)若MN是椭圆E经过 原点的弦,MN||AB,求证: ![]() 为定值
为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com