
【题目】已知数列![]() 的前
的前![]() 项和
项和![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的通项
的通项![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]()
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)由和项求数列通项,注意分类讨论:当![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,最后分析能否合并:
,最后分析能否合并:![]() (Ⅱ)因为
(Ⅱ)因为![]() ,所以数列
,所以数列![]() 的前
的前![]() 项和为两部分求和的和,一部分利用错位相减法求
项和为两部分求和的和,一部分利用错位相减法求![]() 前
前![]() 项和,一部分利用等比数列求和公式求
项和,一部分利用等比数列求和公式求![]() 前
前![]() 项和,利用错位相减法求和时,注意相减时项的符号变化,中间部分利用等比数列求和时注意项数,最后要除以
项和,利用错位相减法求和时,注意相减时项的符号变化,中间部分利用等比数列求和时注意项数,最后要除以![]()
试题解析:(Ⅰ)当![]() 时,
时,![]() …………3分
…………3分
当![]() ,得
,得![]() ,
,![]() (
(![]() ); ……………………………5分
); ……………………………5分
(Ⅱ)由题意知![]() =
=![]()
记![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 的前
的前![]() 项和为
项和为![]() ,…………………6分
,…………………6分
因为![]() =
=![]() ,
,
所以![]()
![]()
两式相减得![]() 2+
2+![]()
![]() =
=![]()
所以![]() , …………………………………………10分
, …………………………………………10分
又![]() , …………………………………………12分
, …………………………………………12分
所以![]()
![]() =
=![]()
=![]() . …………………………………………13分
. …………………………………………13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知各项都是正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:![]() ,
,![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,求证:
,求证:![]() ;
;
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①对立事件一定是互斥事件;
②函数![]() 的最小值为2;
的最小值为2;
③八位二进制数能表示的最大十进制数为256;
④在![]() 中,若
中,若![]() ,
, ![]() ,
, ![]() ,则该三角形有两解.
,则该三角形有两解.
其中正确命题的个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
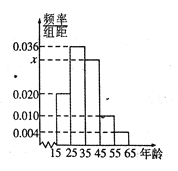
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为![]() ,求△AOB面积的最大值,并求此时直线l的方程.
,求△AOB面积的最大值,并求此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com