练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知等比数列的各项都为正数，且当n≥3时，a4a2n－4＝102n，则数列lga1,2lga2,22lga3,23lga4，…，2n－1lgan，…的前n项和Sn等于(　　)

    A．n·2n                                B．(n－1)·2n－1－1

    C．(n－1)·2n＋1                        D．2n＋1


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


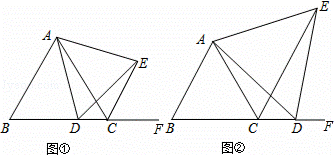
    已知等边△ABC，点D是直线BC上一点，以AD为边在AD的右侧作等边△ADE，连结CE．

    （1）如图①，若点D在线段BC上，求证：CE+CD=AB；

    （2）如图②，若点D在BC延长线上，线段CD，CE和AB有怎样的数量关系？证明你的结论．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝图象上存在不同的三点到原点的距离构成等比数列，则以下不可能成为公比的数是(　　)

    A.                                    B.

    C.                                  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}满足a1＝1，an＋1＝则其前6项之和是(　　)

    A．16                                   B．20

    C．33                                   D．120

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在数列{an}中，，又bn＝，则数列{bn}的前n项和为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若P＝(a≥0)，则P，Q的大小关系(　　)

    A．P>Q                                  B．P＝Q

    C．P<Q                                  D．由a取值决定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn表示数列{an}的前n项和．

    (1)若{an}为等差数列，推导Sn的计算公式；

    (2)若a1＝1，q≠0，且对所有正整数n，有Sn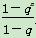＝，判断{an}是否为等比数列，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    观察下列算式：

    13＝1，

    23＝3＋5，

    33＝7＋9＋11，

    43＝13＋15＋17＋19，

    ……

    若某数m3按上述规律展开后，发现等式右边含有“2 013”这个数，则m＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)与g(x)的图象关于直线x＝2对称，若f(x)＝4x－15，则不等式的解集是________．

    查看答案和解析>>

    同步练习册答案