
| A. | 4 | B. | $-\frac{16}{9}$ | C. | -2 | D. | -4 |
分析 如图所示,以PB,PC为邻边作平行四边形PBDC,可得$\overrightarrow{PB}+\overrightarrow{PC}$=$2\overrightarrow{PM}$.由$\overrightarrow{{P}{M}}=2\overrightarrow{{A}{P}}$,可得$\overrightarrow{AP}$=$\frac{1}{3}\overrightarrow{AM}$,$\overrightarrow{PM}=\frac{2}{3}\overrightarrow{AM}$.代入$\overrightarrow{{P}{A}}•({\overrightarrow{{P}{B}}+\overrightarrow{{P}C}})$即可得出.
解答 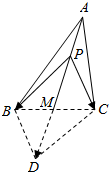 解:如图所示,
解:如图所示,
以PB,PC为邻边作平行四边形PBDC,
则$\overrightarrow{PB}+\overrightarrow{PC}$=$2\overrightarrow{PM}$,
∵AM=3,点P在AM上且满足$\overrightarrow{{P}{M}}=2\overrightarrow{{A}{P}}$,
∴$\overrightarrow{AP}$=$\frac{1}{3}\overrightarrow{AM}$,$\overrightarrow{PM}=\frac{2}{3}\overrightarrow{AM}$.
∴$\overrightarrow{{P}{A}}•({\overrightarrow{{P}{B}}+\overrightarrow{{P}C}})$=-$\frac{1}{3}\overrightarrow{AM}$$•\frac{4}{3}\overrightarrow{AM}$
=$-\frac{4}{9}{\overrightarrow{AM}}^{2}$=-$\frac{4}{9}$×32=-4.
故选:D.
点评 本题考查了数量积运算性质、向量的平行四边形法则、向量共线定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90 | B. | 91 | C. | 99 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -78 | B. | -82 | C. | -148 | D. | -182 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com