
已知函数f(x)=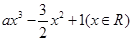 ,其中a>0,
,其中a>0,
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间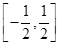 上,f(x)>0恒成立,求a的取值范围。
上,f(x)>0恒成立,求a的取值范围。
(Ⅰ)y=6x-9;(Ⅱ)a的范围为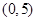 。
。
解析试题分析:(Ⅰ)解:当a=1时,f(x)=
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
已知函数f(x)=ln x-
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
已知f(x)=
科目:高中数学
来源:
题型:解答题
已知函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区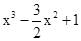 ,f(2)=3;
,f(2)=3;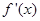 =
=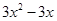 ,
, 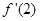 =6.
=6.
所以曲线y=f(x)在点(2,f(2))处的切线方程为y-3=6(x-2),即y=6x-9
(Ⅱ)解: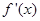 =
=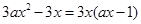 .令f’(x)=0,解得x=0或x=
.令f’(x)=0,解得x=0或x=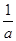 . 5分
. 5分
以下分两种情况讨论:
(1)若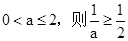 ,当x变化时,
,当x变化时,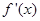 ,f(x)的变化情况如表:
,f(x)的变化情况如表:
当x 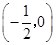
0 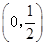
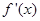
+ 0 - f(x) 
极大值 
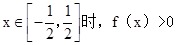 等价于
等价于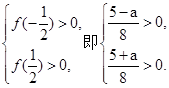
解不等式组得-5<a<5.因此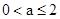 .
.
若a>2,则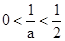 .当x变化时,
.当x变化时,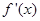 , f(x)的变化情况如下表:
, f(x)的变化情况如下表:x 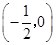
0 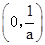
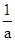
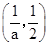
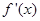
+ 0 - 

复习与测评单元综合测试卷系列答案
小学毕业总复习北京教育出版社系列答案
名校有约小学毕业升学总复习系列答案
初中毕业升学考试指南系列答案
组合阅读训练系列答案
名校名师测试卷系列答案
期末复习第1卷系列答案
初中毕业生升学考试复习用书系列答案
阶段性同步复习与测试系列答案
创新学案课时作业测试卷系列答案
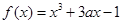 ,
,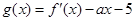 ,其中
,其中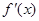 是
是 的导函数.
的导函数.
(1)对满足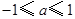 的一切
的一切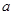 的值,都有
的值,都有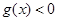 ,求实数
,求实数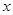 的取值范围;
的取值范围;
(2)设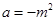 ,当实数
,当实数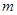 在什么范围内变化时,函数
在什么范围内变化时,函数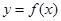 的图象与直线
的图象与直线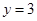 只有一个公共点.
只有一个公共点.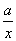 .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为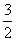 ,求a的值;
,求a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求a的取值范围.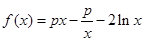 .
.
(1)若p=2,求曲线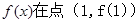 处的切线方程;
处的切线方程;
(2)若函数在其定义域内是增函数,求正实数p的取值范围;
(3)设函数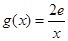 ,若在[1,e]上至少存在一点
,若在[1,e]上至少存在一点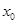 ,使得
,使得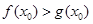 成立,求实
成立,求实
数p的取值范围. (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.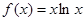 ,
,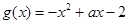
(1)求函数 在
在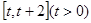 上的最小值;
上的最小值;
(2)若函数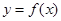 与
与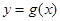 的图像恰有一个公共点,求实数a的值;
的图像恰有一个公共点,求实数a的值;
(3)若函数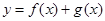 有两个不同的极值点
有两个不同的极值点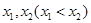 ,且
,且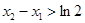 ,求实数a的取值范围。
,求实数a的取值范围。
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号