
【题目】设x取实数,则f(x)与g(x)表示同一个函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)= ![]() ,g(x)=
,g(x)= ![]()
C.f(x)=1,g(x)=(x﹣1)0
D.f(x)= ![]() ,g(x)=x﹣3
,g(x)=x﹣3
【答案】B
【解析】解:A组中两函数的定义域相同,对应关系不同,g(x)=|x|≠x,故A中的两函数不为同一个函数;B组中两函数的定义域均为所有正数构成的集合,对应关系化简为f(x)=g(x)=1,故B中的两函数是同一个函数;
C组中两函数的定义域不同,f(x)的定义域为R,g(x)的定义域为{x|x≠1},故C中的两函数不为同一个函数;
D组中两函数的定义域不同,g(x)的定义域为R,f(x)的定义域由不等于﹣3的实数构成,故D中的两函数不为同一个函数.
故选B.
根据确定函数的三要素判断每组函数是否为同一个函数,即需要确定每组函数的定义域、对应关系、值域是否相同,也可只判断前两项是否相同即可确定这两个函数是否为同一个函数.


科目:高中数学 来源: 题型:
【题目】盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球.规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得![]() 分,现从盒内任取3个球.
分,现从盒内任取3个球.
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设![]() 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某天数学课上,你突然惊醒,发现黑板上有如下内容:
例:求x3﹣3x,x∈[0,+∞)的最小值.解:利用基本不等式a+b+c≥3 ![]() ,得到x3+1+1≥3x,于是x3﹣3x=x3+1+1﹣3x﹣2≥3x﹣3x﹣2=﹣2,当且仅当x=1时,取到最小值﹣2
,得到x3+1+1≥3x,于是x3﹣3x=x3+1+1﹣3x﹣2≥3x﹣3x﹣2=﹣2,当且仅当x=1时,取到最小值﹣2
(1)老师请你模仿例题,研究x4﹣4x,x∈[0,+∞)上的最小值;
(提示:a+b+c+d≥4 ![]() )
)
(2)研究 ![]() x3﹣3x,x∈[0,+∞)上的最小值;
x3﹣3x,x∈[0,+∞)上的最小值;
(3)求出当a>0时,x3﹣ax,x∈[0,+∞)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]()
(1)求证f(x)在(0,+∞)上递增
(2)若f(x)在[m,n]上的值域是[m,n],求实数a的取值范围
(3)当f(x)≤2x在(0,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
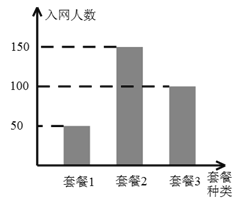
【题目】移动公司在春节正月初八这天推出4G套餐,对这天办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元. 初八当天参与活动的人数统计结果如图所示,
(Ⅰ)从参加当天活动的人中任选一人,求此人获得优惠金额不低于300元的概率(将频率视为概率);
(Ⅱ)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选两人,求这两人获得相等优惠金额的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com