
����Ŀ��ij����ѧ���ϣ���ͻȻ���ѣ����ֺڰ������������ݣ�
������x3��3x��x��[0��+�ޣ�����Сֵ���⣺���û�������ʽa+b+c��3 ![]() ���õ�x3+1+1��3x������x3��3x=x3+1+1��3x��2��3x��3x��2=��2�����ҽ���x=1ʱ��ȡ����Сֵ��2
���õ�x3+1+1��3x������x3��3x=x3+1+1��3x��2��3x��3x��2=��2�����ҽ���x=1ʱ��ȡ����Сֵ��2
��1����ʦ����ģ�����⣬�о�x4��4x��x��[0��+�ޣ��ϵ���Сֵ��
����ʾ��a+b+c+d��4 ![]() ��
��
��2���о� ![]() x3��3x��x��[0��+�ޣ��ϵ���Сֵ��
x3��3x��x��[0��+�ޣ��ϵ���Сֵ��
��3�������a��0ʱ��x3��ax��x��[0��+�ޣ�����Сֵ��
���𰸡�
��1���⣺x4��4x=x4+1+1+1��4x��3��4x��4x��3=��3�����ҽ���x=1ʱ��ȡ����Сֵ��3
��2���⣺ ![]() x3��3x=
x3��3x= ![]() x3+3+3��3x��6��3x��3x��6=��6�����ҽ���x=3ʱ��ȡ����Сֵ��6
x3+3+3��3x��6��3x��3x��6=��6�����ҽ���x=3ʱ��ȡ����Сֵ��6
��3���⣺x3��ax=x3+ ![]() +
+ ![]() ��ax��
��ax�� ![]() ��ax��ax��
��ax��ax�� ![]() =��
=�� ![]() �����ҽ���x=
�����ҽ���x= ![]() ʱ��ȡ����Сֵ��
ʱ��ȡ����Сֵ�� ![]()
����������1�������¶���ɵ�x4��4x=x4+1+1+1��4x��3����ü��ɣ���2�������¶���ɵ� ![]() x3��3x=
x3��3x= ![]() x3+3+3��3x��6����ü��ɣ���3�������¶���ɵ�x3��ax=x3+
x3+3+3��3x��6����ü��ɣ���3�������¶���ɵ�x3��ax=x3+ ![]() +
+ ![]() ��ax��
��ax�� ![]() ����ü��ɣ�
����ü��ɣ�
�����㾫�������ջ�������ʽ�ǽ����ĸ�������Ҫ֪����������ʽ��![]()
![]() ,�����ҽ���
,�����ҽ���![]() ʱȡ���Ⱥţ������ι�ʽ��
ʱȡ���Ⱥţ������ι�ʽ��![]()
![]() ��
��


 �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϊ����������{an}��ǰn���ΪSn �� ����4Sn=an+12��4n��1��n��N* �� ��a2 �� a5 �� a14���ɵȱ����У�
��1��֤����a2= ![]() ��
��
��2��������{an}��ͨ�ʽ��
��3��֤������һ��������n���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У�����Բ (
(![]() ����)��������
����)��������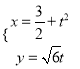 (
(![]() ����).
����).
�����Ƿ����������![]() ֵ��ʹ�ø���Բ������������ĸ���ͬ�Ľ��㣿��˵������.
ֵ��ʹ�ø���Բ������������ĸ���ͬ�Ľ��㣿��˵������.
����![]() ȡ��ֵʱ������Բ��������ߵĽ���������ԭ��ľ������������������Բ���ĵľ��룿
ȡ��ֵʱ������Բ��������ߵĽ���������ԭ��ľ������������������Բ���ĵľ��룿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���f��x��=ax2+2x��2a��������f��x��=0�����������x1 �� x2
��1����a��0����x1��1��x2 �� ��a��ȡֵ��Χ��
��2����x1��1��x2��1ͬ�ţ���a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪c��0��������p������y=cxΪ������������q����x��[ ![]() ��2]ʱ������f��x��=x+
��2]ʱ������f��x��=x+ ![]() ��
�� ![]() ������������p��q��Ϊ�����⣬��p��q��Ϊ�����⣬��c��ȡֵ��Χ�� ��
������������p��q��Ϊ�����⣬��p��q��Ϊ�����⣬��c��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����xȡʵ������f��x����g��x����ʾͬһ���������ǣ� ��
A.f��x��=x��g��x��= ![]()
B.f��x��= ![]() ��g��x��=
��g��x��= ![]()
C.f��x��=1��g��x��=��x��1��0
D.f��x��= ![]() ��g��x��=x��3
��g��x��=x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��֪����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ��
�� ![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1��������![]() ����ͨ����������
����ͨ����������![]() ��ֱ�����귽�̣������������߹�����ĸ�����
��ֱ�����귽�̣������������߹�����ĸ�����
��2����![]() ������������
������������![]() ��
��![]() ����Χ�ɵ��ı�����������ֵ.
����Χ�ɵ��ı�����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������
��������![]() ��
�� ![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����
��������![]() �ļ�ֵ��
�ļ�ֵ��
����![]() ʱ����ֱ��
ʱ����ֱ��![]() ������
������![]() û�й����㣬��
û�й����㣬��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017���ϳ�ɳ��ģ��ij�ֲ�Ʒ��������������ָ��ֵ����������������ָ��ֵ���ֵȼ����±���
����ָ��ֵ |
|
|
|
�ȼ� | ����Ʒ | ����Ʒ | һ��Ʒ |
��ij��ҵ���������ֲ�Ʒ�г�ȡ200��������õ����µ�Ƶ�ʷֲ�ֱ��ͼ��
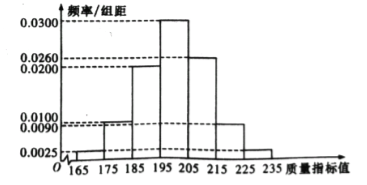
��1���������ϳ����������ݣ��ܷ���Ϊ����ҵ���������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռȫ����Ʒ90%���Ĺ涨��
��2���������У�����Ʒ�ȼ��÷ֲ�����ķ�����ȡ8�����ٴ���8����Ʒ�������ȡ4�������ȡ��4����Ʒ�У�һ����������Ʒ���еĸ��ʣ�
��3������ҵΪ��߲�Ʒ��������չ�ˡ����������¡��������ٳ�����⣬��Ʒ����ָ��ֵ![]() ��������
��������![]() �������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
�������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com