
 如图,在底面半径为2、母线长为4的圆锥中挖去一个高为$\sqrt{3}$的内接圆柱;
如图,在底面半径为2、母线长为4的圆锥中挖去一个高为$\sqrt{3}$的内接圆柱;分析 (1)利用S表面积=2S底+S侧,求圆柱的表面积;
(2)求出三棱锥、圆柱的体积,即可求圆锥挖去圆柱剩下几何体的体积.
解答 解:设圆锥、圆柱的底面半径分别为R、r,高分别为h、h′.
(1)圆锥的高h=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
又∵h′=$\sqrt{3}$,
∴h′=$\frac{1}{2}$h.∴$\frac{r}{2}$=$\frac{2\sqrt{3}-\sqrt{3}}{2\sqrt{3}}$,∴r=1.
∴S表面积=2S底+S侧=2πr2+2πrh′
=2π+2π×$\sqrt{3}$=2(1+$\sqrt{3}$)π.…(6分)
(2)所求体积$V={V_{三棱锥}}-{V_{圆柱}}=\frac{1}{3}π{R^2}•h-π{r^2}•h'=\frac{1}{3}π•{2^2}×2\sqrt{3}-π•{1^2}×\sqrt{3}$=$\frac{5}{3}\sqrt{3}π$…(12分)
点评 本题考查圆柱的表面积、三棱锥、圆柱的体积,考查学生的计算能力,比较基础.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:选择题
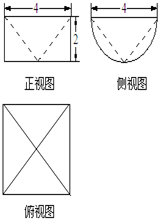
| A. | 16π-$\frac{16}{3}$ | B. | 16π-$\frac{32}{3}$ | C. | 8π-$\frac{16}{3}$ | D. | 8π-$\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
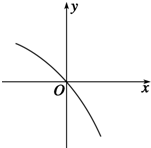 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-2)>1的解集为( )
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-2)>1的解集为( )| A. | (-2,3) | B. | (-2,5) | C. | (0,5) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$-1) | B. | (-∞,2-$\frac{1}{e}$) | C. | [$\frac{1}{e}$-1,+∞) | D. | [2-$\frac{1}{e}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com