Question

【题目】已知函数.

（1）若函数的图象在处的切线过点，求的值；

（2）当时，函数在上没有零点，求实数的取值范围；

（3）当时，存在实数使得，求证：.

Answer 1

【答案】（1）；（2）或；（3）证明见解析.

【解析】分析：（1）先根据导数几何意义得切线斜率，再根据两点间斜率公式列等式，解得的值；（2）先求导数，根据a讨论导数零点情况，再根据对应单调性确定函数值域，最后根据无零点确定最小值大于零或最大值小于零，解得结果，（3）先根据，解得，代入得，再转化为一元函数：最后利用导数证明h(t)< 0成立.

详解：（1）因为f ′(x)＝－a，所以k＝f ′(1)＝1－a，

又因为f(1)＝－a－b，所以切线方程为y＋a＋b＝(1－a)(x－1)，

因为过点(2，0)，所以a＋b=1－a，即2a＋b＝1.

（2）当b＝0时，f(x)＝lnx－ax，所以f ′(x)＝－a＝.

10若a≤0，则f ′(x)＞0，所以f(x)在(，＋∞)上递增，所以f(x)＞f()＝－1－，

因为函数y＝f(x)在(，＋∞)上没有零点，所以－1－≥0，即a≤－e；

20若a＞0，由f ′(x)＝0，得x＝.

①当≤时，即a≥e时，f ′(x)＜0，f(x)在(，＋∞)上递减，

所以f(x)＜f()＝－1－＜0，符合题意，所以a≥e；

②当＞时，即0＜a＜e时，若＜x＜，f ′(x)＜0，f(x)在(，)上递增；

若x＞，f ′(x)＞0，f(x)在(，＋∞)上递减，

所以f(x)在x＝处取得极大值，即为最大值，

要使函数y＝f(x)在(，＋∞)上没有零点，

必须满足f()＝ln－1＝－lna－1＜0，得a＞，所以＜a＜e.

综上所述，实数a的取值范围是a≤－e或a＞.

（3）不妨设0＜x1＜x2，

由f(x1)＝f(x2)，得lnx1－ax1－b＝lnx2－ax2－b，

因为a＞0，所以.

又因为，f ′(x)在(0，＋∞)上递减，且f ′()＝0，

故要证，只要证，

只要证，只要证，

只要证 （*），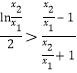

令，记，

则，

所以h(t)在(1,+∞)上递减，所以h(t)< h(1)=0，

所以（*）成立，所以原命题成立.