
在极坐标系中,已知曲线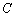 :
: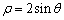 ,过极点O的直线
,过极点O的直线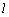 与曲线
与曲线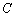 相交于A、B两点,
相交于A、B两点,
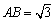 ,求直线
,求直线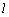 的方程.
的方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
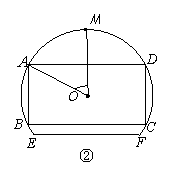
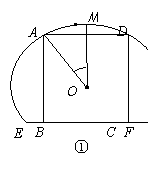
如图,一块弓形薄铁片EMF,点M为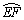 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=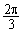 .将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在
.将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在 上,设∠AOD=
上,设∠AOD= .
.
(1)求矩形铁片ABCD的面积S关于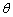 的函数关系式;
的函数关系式;
 (2)当矩形铁片ABCD的
(2)当矩形铁片ABCD的 面积最大时,求cos
面积最大时,求cos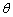 的值.
的值.
 |  | ||
查看答案和解析>>
科目:高中数学 来源: 题型:
下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是
A.30.5 B.31.5 C.31 D.32
| 1 | 0 | 2 | ||
| 2 | 0 | 1 | 4 | |
| 3 | 1 | 1 | 2 | 6 |
| 4 | 3 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
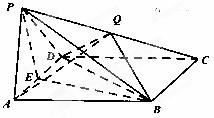
如图,四棱锥P—ABCD中,底面ABCD是菱形,PA= PD,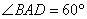 ,E是AD的中点,点Q在侧棱PC上.
,E是AD的中点,点Q在侧棱PC上.
(Ⅰ)求证:AD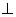 平面PBE;
平面PBE;
(Ⅱ)若Q是PC的中点,求证:PA∥平面BDQ;
(Ⅲ)若 ,试求
,试求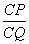 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com