
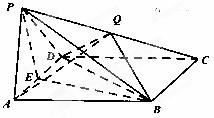
如图,四棱锥P—ABCD中,底面ABCD是菱形,PA= PD,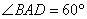 ,E是AD的中点,点Q在侧棱PC上.
,E是AD的中点,点Q在侧棱PC上.
(Ⅰ)求证:AD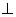 平面PBE;
平面PBE;
(Ⅱ)若Q是PC的中点,求证:PA∥平面BDQ;
(Ⅲ)若 ,试求
,试求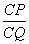 的值.
的值.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
下列说法错误的是 ( )
A.命题:“已知f(x)是R 上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题
上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题
B.“x>1”是“|x|>1”的充分不必要条件 C.若p且q为假命题, 则p、q均为假命题
则p、q均为假命题
 D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+
D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+ 1≥0”
1≥0”

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com