
科目:高中数学 来源: 题型:解答题
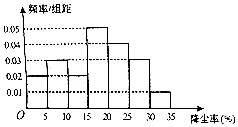 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{64}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
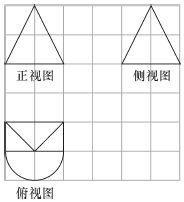 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )| A. | $({1+\frac{{\sqrt{5}}}{2}})•π+2({1+\sqrt{5}})$ | B. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({1+\sqrt{5}})$ | C. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({3+\sqrt{5}})$ | D. | $\frac{{({1+\sqrt{5}})}}{2}•π+4+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )| A. | -2 | B. | 2 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com