
分析 (1)由A与B的交集为B,得B为A的子集,确定出m的范围即可;
(2)根据A与B的交集不为空集,确定出m的范围即可.
解答 解:(1)∵A∩B=B,∴B⊆A,
∵A={x|-4<x<2},B={x|m-1<x<m+1},
∴$\left\{\begin{array}{l}{m-1≥-4}\\{m+1≤2}\end{array}\right.$,
解得:-3≤m≤1,
则m的取值集合为[-3,1];
(2)∵A={x|-4<x<2},B={x|m-1<x<m+1},A∩B≠∅,
∴若A∩B=∅时,
由B≠∅,得到m-1≥2或m+1≤-4,
解得:m≥3或m≤-5,
则A∩B≠∅时,m的取值集合为(-5,3).
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$∞,\frac{1}{5}$)∪[$\frac{2}{5},+∞$] | B. | [0,$\frac{1}{5}$] | C. | (0,$\frac{1}{5}$] | D. | (-$∞,\frac{1}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
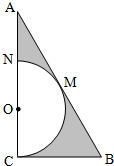 如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.
如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com