
| ||
| 43 |
| 3 |
| 8 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
| ||
| 43 |
| 3 |
| 8 |
| 33 |
| 43 |
| 27 |
| 64 |
| ||
| 43 |
| 27 |
| 64 |
3•
| ||
| 43 |
| 9 |
| 64 |
| ||
| 43 |
| 1 |
| 64 |
| ζ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|


科目:高中数学 来源: 题型:
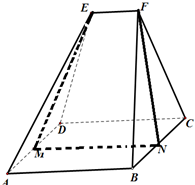 木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6| 2 |
| ||
| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
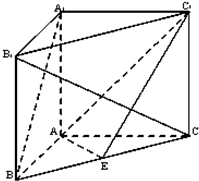 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| A1An+1 |
| BnCn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com