
 已知函数f(x)=-mcos(ωx+φ)(m>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,点A,B,C为f(x)的图象与坐标轴的交点,且A(1,0),D($\frac{5}{3}$,-$\frac{10}{3}$),$\overrightarrow{CD}$=$\frac{1}{2}$$\overrightarrow{DB}$,则m=5$\sqrt{2}$.
已知函数f(x)=-mcos(ωx+φ)(m>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,点A,B,C为f(x)的图象与坐标轴的交点,且A(1,0),D($\frac{5}{3}$,-$\frac{10}{3}$),$\overrightarrow{CD}$=$\frac{1}{2}$$\overrightarrow{DB}$,则m=5$\sqrt{2}$. 分析 根据题意,利用平面向量的坐标表示与运算,求出|AB|的值,从而求出函数f(x)的周期T与ω的值,再求出φ与m的值即可.
解答 解:设点B(x,0),C(0,y),又点D($\frac{5}{3}$,-$\frac{10}{3}$),
∴$\overrightarrow{CD}$=($\frac{5}{3}$,-$\frac{10}{3}$-y),$\overrightarrow{DB}$=(x-$\frac{5}{3}$,$\frac{10}{3}$);
又$\overrightarrow{CD}$=$\frac{1}{2}$$\overrightarrow{DB}$,
∴$\left\{\begin{array}{l}{\frac{5}{3}=\frac{1}{2}(x-\frac{5}{3})}\\{-\frac{10}{3}-y=\frac{1}{2}×\frac{10}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=-5}\end{array}\right.$,
即点B(5,0),C(0,-5),所以|AB|=4;
所以T=$\frac{2π}{ω}$=2|AB|=8,
解得ω=$\frac{π}{4}$,
所以f(x)=-mcos($\frac{π}{4}$x+φ);
把点A(1,0)代入f(x)可得,cos($\frac{π}{4}$+φ)=0,
所以$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,k∈Z,
即φ=kπ+$\frac{π}{4}$,k∈Z,
又|φ|<$\frac{π}{2}$,所以φ=$\frac{π}{4}$,
所以-mcos$\frac{π}{4}$=-5,解得m=5$\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了平面向量的坐标表示与运算问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
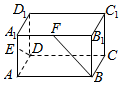 如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )
如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com