
【题目】设函数![]() .
.
(1)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)求导得![]() ,故根据
,故根据![]() 的符号可判断函数的单调性.(2)结合(1)中的函数的单调性求解,当
的符号可判断函数的单调性.(2)结合(1)中的函数的单调性求解,当![]() 时
时![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,且
单调递减,且![]() ,故要有两个零点,则需
,故要有两个零点,则需![]() ,解不等式可得结果;当
,解不等式可得结果;当![]() 时,可得
时,可得![]() 单调递增,而
单调递增,而![]() ,所以
,所以![]() 在
在![]() 上有一个零点0,不合题意.由此可得所求范围为
上有一个零点0,不合题意.由此可得所求范围为![]() .
.
详解:( 1)∵![]() ,
,
∴![]() .
.
令![]() ,则
,则![]() .
.
∴![]() 有两不等实根
有两不等实根![]() ,
,![]() .
.
且当![]() 或
或![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)解法1:
①当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
∵![]() 在
在![]() 上有两个零点,且
上有两个零点,且![]() ,
,
∴![]() ,解得
,解得![]() .
.
②当![]() 时,若
时,若![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增,而
单调递增,而![]() ,所以因为
,所以因为![]() 在
在![]() 上有一个零点0.
上有一个零点0.
综上得当![]() 在
在![]() 上有两个零点时,实数
上有两个零点时,实数![]() 的取值范围为
的取值范围为![]() .
.
解法2:
①当![]() 时,若
时,若![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
又![]() ,
,
∴![]() 在
在![]() 上有一个零点0.
上有一个零点0.
②当![]() 时,由(1)得
时,由(1)得![]() ,
,![]() .
.
(ⅰ)若![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增.
单调递增.
又![]() ,
,
∴![]() 在
在![]() 上只有一个零点.
上只有一个零点.
(ⅱ)若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∵![]() ,
,
∴若![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() ,解得
,解得![]() .
.
综上得当![]() 在
在![]() 上有两个零点时,实数
上有两个零点时,实数![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 为
为![]() 的中点,且有
的中点,且有![]() ,现以
,现以![]() 为折痕,将
为折痕,将![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
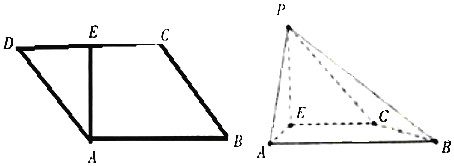
(1)证明:![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上运动(不包括线段端点),且
上运动(不包括线段端点),且![]() .以下结论:①
.以下结论:①![]() ;②若点
;②若点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则由线
的中点,则由线![]() 与
与![]() 确定的平面在正方体
确定的平面在正方体![]() 上的截面为等边三角形;③四面体
上的截面为等边三角形;③四面体![]() 的体积的最大值为
的体积的最大值为![]() ;④直线
;④直线![]() 与直线
与直线![]() 的夹角为定值.其中正确的结论为______.(填序号)
的夹角为定值.其中正确的结论为______.(填序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量y(单位:万只)与相成年份x(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数z(单位:个)关于x的回归方程![]() .
.

(1)根据表中的数据和所给统计量,求y关于x的线性回归方程(参考统计量:![]() );
);
(2)试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是其左、右焦点,且过点
分别是其左、右焦点,且过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若在直线![]() 上任取一点
上任取一点![]() ,从点
,从点![]() 向
向![]() 的外接圆引一条切线,切点为
的外接圆引一条切线,切点为![]() .问是否存在点
.问是否存在点![]() ,恒有
,恒有![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: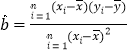 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com