
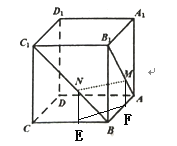
【题目】棱长为1的正方体![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上运动(不包括线段端点),且
上运动(不包括线段端点),且![]() .以下结论:①
.以下结论:①![]() ;②若点
;②若点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则由线
的中点,则由线![]() 与
与![]() 确定的平面在正方体
确定的平面在正方体![]() 上的截面为等边三角形;③四面体
上的截面为等边三角形;③四面体![]() 的体积的最大值为
的体积的最大值为![]() ;④直线
;④直线![]() 与直线
与直线![]() 的夹角为定值.其中正确的结论为______.(填序号)
的夹角为定值.其中正确的结论为______.(填序号)

【答案】① ② ③
【解析】
①作NE⊥BC,MF⊥AB,垂足分别为E,F,可得四边形MNEF是矩形,可得MN∥FE,利用AA1⊥面AC,可得结论成立;
②截面为△AB1C,为等边三角形,故正确.
③设![]()
![]() ,则
,则![]() =
=![]() dM﹣BCN=
dM﹣BCN=![]() ,故③成立;
,故③成立;
④设![]()
![]() ,当
,当![]() 接近于0时,直线
接近于0时,直线![]() 与直线
与直线![]() 的夹角接近于
的夹角接近于![]() ,当
,当![]() 接近于1时,夹角接近于
接近于1时,夹角接近于![]() ,故④不正确;
,故④不正确;
①作NE⊥BC,MF⊥AB,垂足分别为E,F,∵AM=BN,∴NE=MF,∴四边形MNEF是矩形,∴MN∥FE,∵AA1⊥面AC,EF面AC,∴AA1⊥EF,∴AA1⊥MN,故①正确;
②点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD﹣A1B1C1D1 上的截面为△AB1C,为等边三角形,故②正确.
③设![]()
![]() ,则
,则![]() =
=![]() dM﹣BCN,又AM=BN=
dM﹣BCN,又AM=BN=![]() ,
,
∴![]() =
=![]() ,dM﹣BCN =
,dM﹣BCN =![]() ,∴
,∴![]() =
=![]() dM﹣BCN=
dM﹣BCN=![]() ,当且仅当
,当且仅当![]() 时取得最大值,故③成立;
时取得最大值,故③成立;
④设![]()
![]() ,当
,当![]() 接近于0时,直线
接近于0时,直线![]() 与直线
与直线![]() 的夹角近似于直线
的夹角近似于直线![]() 和直线
和直线![]() 的夹角,接近于
的夹角,接近于![]() ,当
,当![]() 接近于1时,直线
接近于1时,直线![]() 与直线
与直线![]() 的夹角近似于直线
的夹角近似于直线![]() 和直线
和直线![]() 的夹角,接近于
的夹角,接近于![]() ,故④不正确;
,故④不正确;
综上可知,正确的结论为①②③
故答案为:①②③


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号 | 分组(分数) | 组中值 | 频数(人数) | 频率 |
1 |
| 65 | ① | 0.12 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.24 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1 |
(1)填充频率分布表中的空格;
(2)规定成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名同学获奖?
(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜.投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.现由甲先投.
,且各次投篮互不影响.现由甲先投.
(1)求甲获胜的概率;
(2)求投篮结束时甲的投篮次数X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(I)若曲线![]() ,参数方程为:
,参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程
的普通方程
(Ⅱ)若曲线![]() ,参数方程为
,参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() ,与曲线
,与曲线![]() 交点分别为
交点分别为![]() ,求
,求![]() 的取值范围,
的取值范围,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() ,其长轴是短轴的两倍,以某短轴顶点和长轴顶点为端点的线段作为直径的圆的周长为
,其长轴是短轴的两倍,以某短轴顶点和长轴顶点为端点的线段作为直径的圆的周长为![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .若
.若![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(3)设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,其中
,其中![]() 且
且![]() .设
.设![]() 的面积为
的面积为![]() .以
.以![]() 、
、![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
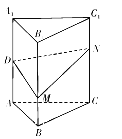
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com