
【题目】甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜.投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.现由甲先投.
,且各次投篮互不影响.现由甲先投.
(1)求甲获胜的概率;
(2)求投篮结束时甲的投篮次数X的分布列与期望.
【答案】(1)![]() ;(2)分布列见解析,数学期望为
;(2)分布列见解析,数学期望为![]()
【解析】
试题分析:(1)本题考查互斥事件的概率,设甲第i次投中获胜的事件为Ai (i=1,2,3),则A1,A2,A3彼此互斥,分别计算出![]() 的概率(可用相互独立事件同时发生的概率公式计算),然后相加即得;
的概率(可用相互独立事件同时发生的概率公式计算),然后相加即得;
(2)甲的投篮次数X的取舍分别1,2,3,注意这里事件![]() 含甲第
含甲第![]() 次投中和第
次投中和第![]() 次投不中而接着乙投中,结合(1)的过程可很快求和各事件概率,从而得分布列,并依据期望公式可计算出期望值.
次投不中而接着乙投中,结合(1)的过程可很快求和各事件概率,从而得分布列,并依据期望公式可计算出期望值.
试题解析:(1)设甲第i次投中获胜的事件为Ai(i=1,2,3),则A1,A2,A3彼此互斥.
甲获胜的事件为A1+A2+A3.
P(A1)=![]() ;
;
P(A2)=![]() ;
;
P(A3)=(![]() )2×(
)2×(![]() )2×
)2×![]() =
=![]() .
.
所以P(A1+A2+A3)=P(A1)+P(A2)+P(A3)=![]() +
+![]() +
+![]() =
=![]() .
.
答:甲获胜的概率为![]() .
.
(2)X所有可能取的值为1,2,3.
则 P(X=1)=![]() +
+![]() ×
×![]() =
=![]() ;
;
P(X=2)=![]() +
+![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() ;
;
P(X=3)=(![]() )2×(
)2×(![]() )2×1=
)2×1=![]() .
.
即X的概率分布列为
X | 1 | 2 | 3 |
P |
|
|
|
所以X的数学期望E(X)=1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】5名男生3名女生参加升旗仪式:
(1)站两横排,3名女生站前排,5名男生站后排有多少种站法?
(2)站两纵列,每列4人,每列都有女生且女生站在男生前面,有多少种排列方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 为
为![]() 的中点,且有
的中点,且有![]() ,现以
,现以![]() 为折痕,将
为折痕,将![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
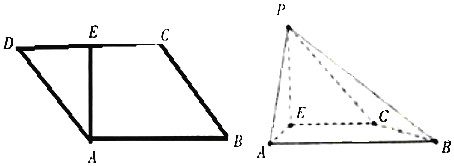
(1)证明:![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分150分),每个班级20名同学,现有甲、乙两位同学的20次成绩如下列茎叶图所示:

(I)根据基叶图求甲、乙两位同学成绩的中位数,并将乙同学的成绩的频率分布直方图填充完整;

(Ⅱ)根据基叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可)
(Ⅲ)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设事件![]() 为“其中2 个成绩分别属于不同的同学”,求事件
为“其中2 个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上运动(不包括线段端点),且
上运动(不包括线段端点),且![]() .以下结论:①
.以下结论:①![]() ;②若点
;②若点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则由线
的中点,则由线![]() 与
与![]() 确定的平面在正方体
确定的平面在正方体![]() 上的截面为等边三角形;③四面体
上的截面为等边三角形;③四面体![]() 的体积的最大值为
的体积的最大值为![]() ;④直线
;④直线![]() 与直线
与直线![]() 的夹角为定值.其中正确的结论为______.(填序号)
的夹角为定值.其中正确的结论为______.(填序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com