
| A. | 3-ln2 | B. | 3ln2 | C. | 2$\sqrt{2}$ | D. | 3 |
分析 换底公式得到$lo{g}_{4}x=-lo{g}_{\frac{1}{4}}x$,然后令f(x)=0,从而得出$x-3=lo{g}_{\frac{1}{4}}x,x>0$,$x+3=(\frac{1}{4})^{x},x≤0$,然后画出直线y=x-3,y=x,y=x+3以及函数$y=lo{g}_{\frac{1}{4}}x$和$y=(\frac{1}{4})^{x}$的图象,由图象可看出|x1-x2|为A,B两点距离的一半,从而求出|x1-x2|的值.
解答 解:$lo{g}_{4}x=-lo{g}_{\frac{1}{4}}x$;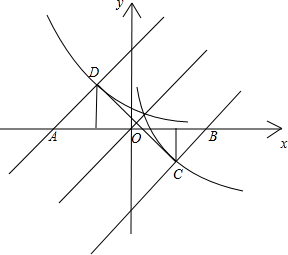
∴令f(x)=0得:
$x-3=lo{g}_{\frac{1}{4}}x,x+3=(\frac{1}{4})^{x}$;
∴直线y=x-3和曲线$y=lo{g}_{\frac{1}{4}}x$的交点C横坐标为x1,直线y=x+3和曲线$y=(\frac{1}{4})^{x}$的交点D横坐标为x2;
如图,两曲线关于y=x对称,直线y=x-3和y=x+3关于y=x对称;
∴CD⊥AD,CD⊥CB;
∴$|{x}_{1}-{x}_{2}|=\frac{|AB|}{2}=3$.
故选:D.
点评 考查函数零点的概念,函数的零点和直线与曲线交点的关系,互为反函数的两图象的对称性,以及数形结合解题的方法.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将1,2,3,…,12无重复地填在如图的12个空格中,要求每一行的数从左到右逐渐增大,每一列的数从上到下逐渐增大,且5和6已经填好,固定在图中的位置上时,符合要求的填法共有9种.
将1,2,3,…,12无重复地填在如图的12个空格中,要求每一行的数从左到右逐渐增大,每一列的数从上到下逐渐增大,且5和6已经填好,固定在图中的位置上时,符合要求的填法共有9种.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com