Question

10．已知f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（x+5）+\frac{4}{3}（x+1），-4≤x≤-1}\\{2|x-1|-2，-1＜x≤4}\end{array}\right.$，g（x）=-$\frac{1}{8}$x²-x+2（-4≤x≤4）给出下列四个命题：
①函数y=f[g（x）]有且只有三个零点；②函数y=g[f（x）]有且只有三个零点；
③函数y=f[f（x）]有且只有六个零点；④函数y=g[g（x）]有且只有一个零点．
其中正确命题的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 分别求出f（x），g（x）的单调性与值域，利用函数的单调性得出复合函数的单调性，即可得出零点个数．

解答 解：f（x）在[-4，-1]上是增函数，在（-1，1]上是减函数，在[1，4]是增函数，
且f（-4）=-4，f（-1）=2，f（1）=-2，f（4）=4．
∴f（x）在区间（-4，-1），（-1，1），（1，4）上各有1个零点，且f（x）的值域为[-4，4]．
设f（x）的三个零点分别为x₁，x₂，x₃，∵f（-3）=log₂2-$\frac{8}{3}$＜0，f（-2）=log₂3-$\frac{4}{3}$＞0，
∴-3＜x₁＜-2，令2|x-1|-2=0得x₂=0，x₃=1．
作出f（x）的大致函数图象如图所示：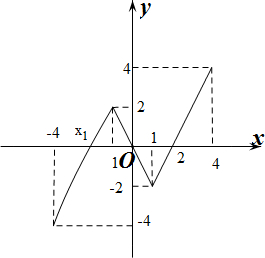

做出y=g（x）的函数图象如图所示：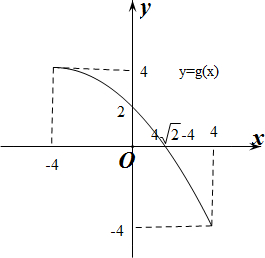

显然g（x）在[-4，4]上为减函数，且g（x）的值域为[-4，4]．
令g（x）=0得x=4$\sqrt{2}$-4，故g（x）的零点为4$\sqrt{2}$-4．
（1）设f[f（x）]=0，则f（x）=x₁，或f（x）=0，或f（x）=2．
∵-3＜x₁＜-2，
由y=f（x）的函数图象可知f（x）=x₁只有一解，f（x）=0有三解，f（x）=2有两解，
∴f[f（x）]有六个零点，故③正确．
（2）设f[g（x）]=0则g（x）=x₁或g（x）=0或g（x）=2，
显然以上方程各有一解，∴f[g（x）]由三个零点，故①正确．
（3）设g[f（x）]=0，则f（x）=4$\sqrt{2}$-4，
∵0$＜4\sqrt{2}-4＜2$，由f（x）的函数图象可知f（x）=4$\sqrt{2}$-4有三个解，
∴g[f（x）]有三个零点，故②正确．
（4）设g[g（x）]=0，则g（x）=4$\sqrt{2}$-4，
由g（x）的函数图象可知g（x）=4$\sqrt{2}-4$有一解，
∴g[g（x）]有一个零点，故④正确．
故选：D．

点评 本题考查了基本初等函数的图象，函数的零点与函数图象的关系，属于中档题．