[题目]根据下列条件.求圆的方程(1)求经过两点 .且圆心在y轴上的圆的方程,(2)圆的的半径为1.圆心与点(1.0)关于对称的圆的方程. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】根据下列条件，求圆的方程
（1）求经过两点，且圆心在y轴上的圆的方程；
（2）圆的的半径为1，圆心与点（1，0）关于对称的圆的方程.

【答案】
（1）解：设圆心的坐标为（0，b），由题意知

，解之得 b=1 圆心坐标为（0,1）

∴

∴圆的方程为

（2）解：设圆心坐标为（a,b）,由题意得

，圆心坐标为

∴圆的方程为

【解析】本题主要考查了圆的标准方程，解决问题的关键是（1）中求圆的方程采用待定系数法，设出方程，代入条件解方程组即可（2）中求圆的方程主要是确定圆心，根据点的对称性求解圆心坐标，求解时设出圆心，利用对称直线是圆心线的垂直平分线求解圆心
【考点精析】根据题目的已知条件，利用圆的标准方程的相关知识可以得到问题的答案，需要掌握圆的标准方程：；圆心为A(a,b),半径为r的圆的方程．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=|mx|﹣|x﹣n|（0＜n＜1+m），若关于x的不等式f（x）＜0的解集中的整数恰有3个，则实数m的取值范围为（）
A.3＜m＜6
B.1＜m＜3
C.0＜m＜1
D.﹣1＜m＜0

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x2lnx﹣a（x2﹣1），a∈R，若当x≥1时，f（x）≥0恒成立，则a的取值范围是（）
A.（﹣∞，﹣1]
B.（﹣∞，0]
C.（﹣∞，1]
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】直线y=x+b与曲线有且只有一个交点，则的取值范围是（）
A.
B. 或
C. 或
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某海滨游乐场出租快艇的收费办法如下：不超过十分钟收费80元；超过十分钟，超过部分按每分钟10元收费（对于其中不足一分钟的部分，若小于0.5分钟则不收费，若大于或等于0.5分钟则按一分钟收费），小茗同学为该游乐场设计了一款收费软件，程序框图如图所示，其中x（分钟）为航行时间，y（元）为所收费用，用[x]表示不大于x的最大整数，则图中①处应填（）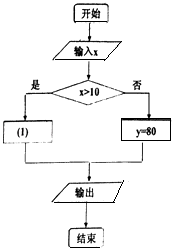

A.y=10[x]
B.y=10[x]﹣20
C.y=10[x﹣ ]﹣20
D.y=10[x+ ]﹣20

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇，网购成了大众购物的一个重要组成部分，可人们在开心购物的同时，假冒伪劣产品也在各大购物网站频频出现，为了让顾客能够在网上买到货真价实的好东西，各大购物平台也推出了对商品和服务的评价体系，现从某购物网站的评价系统中选出100次成功的交易，并对其评价进行统计，对商品的好评率为，对服务的好评率为，其中对商品和服务都做出好评的交易为30次．
（1）列出关于商品和服务评价的2×2列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为商品好评与服务好评有关？
（2）若针对商品的好评率，采用分层抽样的方式从这100次交易中取出5次交易，并从中选择两次交易进行客户回访，求只有一次好评的概率．