
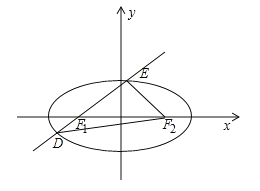
【题目】如图,已知椭圆![]() ,
,![]() 分别为其左、右焦点,过
分别为其左、右焦点,过![]() 的直线与此椭圆相交于
的直线与此椭圆相交于![]() 两点,且
两点,且![]() 的周长为8,椭圆
的周长为8,椭圆![]() 的离心率为
的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在平面直角坐标系![]() 中,已知点
中,已知点![]() 与点
与点![]() ,过
,过![]() 的动直线
的动直线![]() (不与
(不与![]() 轴平行)与椭圆相交于
轴平行)与椭圆相交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点.求证:
轴的对称点.求证:
(i)![]() 三点共线.
三点共线.
(ii)![]() .
.
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() 是过定点
是过定点![]() 且倾斜角为
且倾斜角为![]() 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程,并将曲线
的参数方程,并将曲线![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线![]() 与直线
与直线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“
为“![]() ﹣摆动数列”.
﹣摆动数列”.
①若![]() ,
,![]() ,
,![]() ,则数列
,则数列![]() _____“
_____“![]() ﹣摆动数列”,
﹣摆动数列”,![]() _____“
_____“![]() ﹣摆动数列”(回答是或不是);
﹣摆动数列”(回答是或不是);
②已知“![]() ﹣摆动数列”
﹣摆动数列”![]() 满足
满足![]() ,
,![]() .则常数
.则常数![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为F,过点F作垂直于x轴的直线与抛物线交于A,B两点,且以线段AB为直径的圆过点
的焦点为F,过点F作垂直于x轴的直线与抛物线交于A,B两点,且以线段AB为直径的圆过点![]() .
.
(1)求抛物线C的方程;
(2)设过点![]() 的直线
的直线![]() 分别与抛物线C交于点D,E和点G,H,且
分别与抛物线C交于点D,E和点G,H,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是抛物线y2=4x的焦点,M,P,Q是抛物线上三个不同的动点,直线PM过点F,MQ∥OP,直线QP与MO交于点N.记点M,P,Q的纵坐标分别为y0,y1,y2.
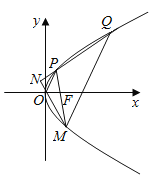
(1)证明:y0=y1﹣y2;
(2)证明:点N的横坐标为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com