
【题目】设F是抛物线y2=4x的焦点,M,P,Q是抛物线上三个不同的动点,直线PM过点F,MQ∥OP,直线QP与MO交于点N.记点M,P,Q的纵坐标分别为y0,y1,y2.
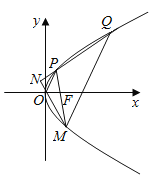
(1)证明:y0=y1﹣y2;
(2)证明:点N的横坐标为定值.
【答案】(1)证明见解析 (2) 证明见解析
【解析】
(1) 由两直线平行的条件:斜率相等,运用直线的斜率公式,结合点在抛物线上,化简可得结论(2) 因为直线![]() 过点
过点![]() ,所以
,所以![]() ,求得直线
,求得直线![]() ,
,![]() 的方程,设点
的方程,设点![]() 坐标为
坐标为![]() ,又因为直线
,又因为直线![]() ,
,![]() 交于点
交于点![]() ,化简整理可得
,化简整理可得![]() ,
,![]() 的方程,分解因式即可得到定值.
的方程,分解因式即可得到定值.
证明:(1) 因为MQ∥OP,所以kMQ=kOP,
所以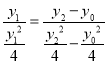 ,所以y0=y1﹣y2;
,所以y0=y1﹣y2;
(2) 因为直线PM过点F,
可得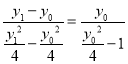 ,
,
所以y1y0=﹣4,
由(1)得y0=y1﹣y2,所以y1![]() ,y2
,y2![]() y0,
y0,
因为OM:y![]() x,
x,
PQ:y﹣y1![]() (x
(x![]() ),
),
即4x﹣(y1+y2)y+y1y2=0,
设点N坐标为(m,n),又因为直线QP,MO交于点N,
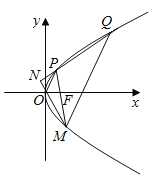
所以n![]() m,4m﹣(y1+y2)n+y1y2=0,
m,4m﹣(y1+y2)n+y1y2=0,
可得y0![]() ,4m﹣(
,4m﹣(![]() y0)n+(
y0)n+(![]() )(
)(![]() y0)=0,
y0)=0,
消去y0得2mn2+n2+8m3+4m2=0,
所以(2m+1)n2+4m2(2m+1)=0,
所以(2m+1)(n2+4m2)=0,
因为n2+4m2≠0,
所以2m+1=0,即m![]() ,
,
所以点N的横坐标为定值![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
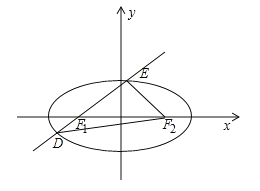
【题目】如图,已知椭圆![]() ,
,![]() 分别为其左、右焦点,过
分别为其左、右焦点,过![]() 的直线与此椭圆相交于
的直线与此椭圆相交于![]() 两点,且
两点,且![]() 的周长为8,椭圆
的周长为8,椭圆![]() 的离心率为
的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在平面直角坐标系![]() 中,已知点
中,已知点![]() 与点
与点![]() ,过
,过![]() 的动直线
的动直线![]() (不与
(不与![]() 轴平行)与椭圆相交于
轴平行)与椭圆相交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点.求证:
轴的对称点.求证:
(i)![]() 三点共线.
三点共线.
(ii)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
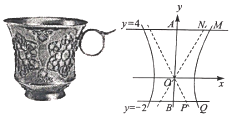
【题目】如图为陕西博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯型几何体的主体部分可近似看作是双曲线![]() 的右支与直线
的右支与直线![]() ,
,![]() ,
,![]() 围成的曲边四边形
围成的曲边四边形![]() 绕
绕![]() 轴旋转一周得到的几何体,如图
轴旋转一周得到的几何体,如图![]() 分别为
分别为![]() 的渐近线与
的渐近线与![]() ,
,![]() 的交点,曲边五边形
的交点,曲边五边形![]() 绕
绕![]() 轴旋转一周得到的几何体的体积可由祖恒原理(祖恒原理:幂势既同,则积不容异).意思是:两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等,那么这两个几何体的体积相等),据此求得该金杯的容积是_____.(杯壁厚度忽略不计)
轴旋转一周得到的几何体的体积可由祖恒原理(祖恒原理:幂势既同,则积不容异).意思是:两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等,那么这两个几何体的体积相等),据此求得该金杯的容积是_____.(杯壁厚度忽略不计)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为A,B,点P在椭圆O上运动,若△PAB面积的最大值为
的左、右顶点分别为A,B,点P在椭圆O上运动,若△PAB面积的最大值为![]() ,椭圆O的离心率为
,椭圆O的离心率为![]() .
.
(1)求椭圆O的标准方程;
(2)过B点作圆E:![]() 的两条切线,分别与椭圆O交于两点C,D(异于点B),当r变化时,直线CD是否恒过某定点?若是,求出该定点坐标,若不是,请说明理由.
的两条切线,分别与椭圆O交于两点C,D(异于点B),当r变化时,直线CD是否恒过某定点?若是,求出该定点坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知动点P与两定点F1(﹣1,0)、F2(1,0)的连线的斜率之积为![]() ,求动点P的轨迹方程.
,求动点P的轨迹方程.
(2)已知双曲线的渐近线方程为y=±![]() x,且与椭圆
x,且与椭圆![]() 1有公共焦点,求此双曲线的标准方程.
1有公共焦点,求此双曲线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面![]() ,直线
,直线![]() .给出下列命题:
.给出下列命题:
① 若![]() ,则
,则![]() ; ② 若
; ② 若![]() ,则
,则![]() ;
;
③ 若![]() ,则
,则![]() ; ④ 若
; ④ 若![]() ,则
,则![]() .
.
其中是真命题的是_________.(填写所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. 288种 B. 144种 C. 720种 D. 360种
查看答案和解析>>
科目:高中数学 来源: 题型:
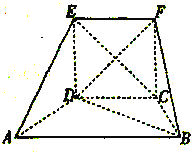
【题目】在如图所示的五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 是正方形,二面角
是正方形,二面角![]() 的大小为
的大小为![]() .
.
(1)在线段![]() 上找出一点
上找出一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com