
【题目】(1)已知动点P与两定点F1(﹣1,0)、F2(1,0)的连线的斜率之积为![]() ,求动点P的轨迹方程.
,求动点P的轨迹方程.
(2)已知双曲线的渐近线方程为y=±![]() x,且与椭圆
x,且与椭圆![]() 1有公共焦点,求此双曲线的标准方程.
1有公共焦点,求此双曲线的标准方程.
科目:高中数学 来源: 题型:
【题目】商品的销售价格与销售量密切相关,为更精准地为商品确定最终售价,商家对商品A按以下单价进行试售,得到如下数据:
单价x(元) | 15 | 16 | 17 | 18 | 19 |
销量y(件) | 60 | 58 | 55 | 53 | 49 |
(1)求销量y关于x的线性回归方程;
(2)预计今后的销售中,销量与单价服从(1)中的线性回归方程,已知每件商品A的成本是10元,为了获得最大利润,商品A的单价应定为多少元?(结果保留整数)
(附: ,
,![]() .(15×60+16×58+17×55+18×53+19×49=4648,152+162+172+182+192=1455)
.(15×60+16×58+17×55+18×53+19×49=4648,152+162+172+182+192=1455)
查看答案和解析>>
科目:高中数学 来源: 题型:
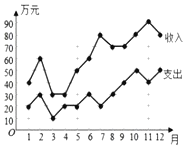
【题目】如图的折线图是某公司2018年1月至12月份的收入与支出数据,若从6月至11月这6个月中任意选2个月的数据进行分析,则这2个月的利润(利润=收入﹣支出)都不高于40万的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个村庄A,B,C构成一个三角形,且AB=5千米,BC=12千米,AC=13千米.为了方便市民生活,现在△ABC内任取一点M建一大型生活超市,则M到A,B,C的距离都不小于2千米的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是抛物线y2=4x的焦点,M,P,Q是抛物线上三个不同的动点,直线PM过点F,MQ∥OP,直线QP与MO交于点N.记点M,P,Q的纵坐标分别为y0,y1,y2.
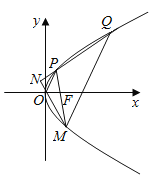
(1)证明:y0=y1﹣y2;
(2)证明:点N的横坐标为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年 份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额(万元) | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长(万元) | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
(1)请用最小二乘法求出y关于x的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额是8万元,估计该公司在该年的年利润增长是多少?(结果保留2位小数)
(2)现从2012—2018年这7年中抽取2年进行调查,记![]() =年利润增长-投资金额,求这两年都是
=年利润增长-投资金额,求这两年都是![]() >2(万元)的概率.
>2(万元)的概率.
参考公式:回归方程![]() 中,
中, 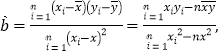
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的偶函数
上的偶函数![]() ,满足
,满足![]() ,且在区间
,且在区间![]() 上是增函数,
上是增函数,
①函数![]() 的一个周期为4;
的一个周期为4;
②直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
③函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
④函数![]() 在
在![]() 内有25个零点;
内有25个零点;
其中正确的命题序号是_____(注:把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某竞赛的题库系统有60%的自然科学类题目,40%的文化生活类题目(假设题库中的题目总数非常大),参赛者需从题库中抽取3个题目作答,有两种抽取方法:方法一是直接从题库中随机抽取3个题目;方法二是先在题库中按照题目类型用分层抽样的方法抽取10个题目作为样本,再从这10个题目中任意抽取3个题目.
(1)两种方法抽取的3个题目中,恰好有1个自然科学类题目和2个文化生活类题目的概率是否相同?若相同,说明理由;若不同,分别计算出两种抽取方法对应的概率.
(2)已知某参赛者抽取的3个题目恰好有1个自然科学类题目和2个文化生活类题目,且该参赛者答对自然科学类题目的概率为![]() ,答对文化生活类题目的概率为
,答对文化生活类题目的概率为![]() .设该参赛者答对的题目数为X,求X的分布列和数学期望.
.设该参赛者答对的题目数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com