
����Ŀ��ij��˾Ϊ���������2012����2018��ÿ����������ڵĸĽ�����Ͷ�ʣ�Ͷ�ʽ�����������������������±���
�� �� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
Ͷ�ʽ���Ԫ�� | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
��������������Ԫ�� | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
��1��������С���˷����y����x�Ļع�ֱ�߷��̣����2019��ù�˾�ƻ����������ڵĸĽ���Ͷ�ʽ����8��Ԫ�����Ƹù�˾�ڸ���������������Ƕ��٣����������2λС����
��2���ִ�2012��2018����7���г�ȡ2����е��飬��![]() =������������Ͷ�ʽ��������궼��
=������������Ͷ�ʽ��������궼��![]() >2����Ԫ���ĸ���.
>2����Ԫ���ĸ���.
�ο���ʽ���ع鷽��![]() �У�
�У� 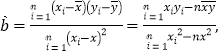
![]()
![]()
���𰸡���1��![]() ��11.43����2��
��11.43����2��![]()
��������
��1�����������ƽ�����ͻع�ϵ����д���ع�ֱ�߷��̣����÷��̼���x��8ʱ![]() ��ֵ���ɣ�
��ֵ���ɣ�
��2����2012��--2018����7��ֱ�Ϊ1,2,3,4,5,6,7�����������оٳ������ܵĻ����¼����ҵ����������ĸ�����������ʼ��ɣ�
��1��![]() ��
��![]() ��
��![]() ��
��
��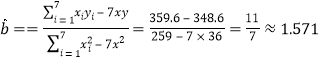 ��
��
![]() ��
��
��ô�ع�ֱ�߷���Ϊ��![]()
��![]() ���뷽�̵�
���뷽�̵�![]()
�����Ƹù�˾�ڸ����������������ԼΪ11.43��Ԫ.
��2���������֪��
��� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| 1.5 | 2 | 1.9 | 2.1 | 2.4 | 2.6 | 3.6 |
��2012��--2018����7��ֱ�Ϊ1,2,3,4,5,6,7�����ܻ����¼�Ϊ����1,2������1,3������1,4������1,5������1,6������1,7������2,3������2,4������2,5������2,6������2,7������3,4������3,5������3,6������3,7������4,5������4,6������4,7������5,6������5,7������6,7��������21�ֽ����
ѡȡ�����궼��![]() ��Ԫ�����Ϊ����4,5������4,6������4,7������5,6������5,7������6,7������6�֣�����ѡȡ�����궼��
��Ԫ�����Ϊ����4,5������4,6������4,7������5,6������5,7������6,7������6�֣�����ѡȡ�����궼��![]() ��Ԫ�ĸ���
��Ԫ�ĸ���![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��4��ֱӪ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �����轫6�����������ֱӪ��������ۣ���ֱӪ����۸û���������������ͳ�����±���ʾ�����ݴ˱����ù�˾����������������ͷ�ʽ��
�����轫6�����������ֱӪ��������ۣ���ֱӪ����۸û���������������ͳ�����±���ʾ�����ݴ˱����ù�˾����������������ͷ�ʽ��

A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������
������![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() .
.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��֤��������![]() ����һ�㴦��������ֱ��
����һ�㴦��������ֱ��![]() ��ֱ��
��ֱ��![]() ��Χ�ɵ������ε����Ϊ��ֵ������˶�ֵ.
��Χ�ɵ������ε����Ϊ��ֵ������˶�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪����P��������F1����1��0����F2��1��0�������ߵ�б��֮��Ϊ![]() ����P�Ĺ켣���̣�
����P�Ĺ켣���̣�
��2����֪˫���ߵĽ����߷���Ϊy����![]() x��������Բ
x��������Բ![]() 1�й������㣬���˫���ߵı����̣�
1�й������㣬���˫���ߵı����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����C�IJ�������Ϊ
�У�����C�IJ�������Ϊ![]() (����
(����![]() Ϊ����)��������ԭ��
Ϊ����)��������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ�У�ֱ��
���������Ϊ���Ὠ��������ϵ�У�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��������C����ͨ���̺�ֱ��![]() ����б�ǣ�
����б�ǣ�
���������![]() (0��2)��
(0��2)��![]() ��
��![]() ����
����![]() ���㣬��
���㣬��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊ��Ȼ�����ĵ���)��
Ϊ��Ȼ�����ĵ���)��
��1����![]() ,����
,����![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ,�ҷ���
,�ҷ���![]() ��
��![]() ���н�,��ʵ��
���н�,��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ����ֱ��
��Բ����ֱ��![]() ��
�� ![]() �ϣ���ֱ��
�ϣ���ֱ��![]() ��
�� ![]() ���У��ҽ�ֱ��
���У��ҽ�ֱ��![]() ��
�� ![]() �����ҳ�Ϊ6
�����ҳ�Ϊ6
������Բ![]() �ķ���
�ķ���
������![]() �Ƿ����ֱ��
�Ƿ����ֱ��![]() ��ʹ��
��ʹ��![]() ��Բ
��Բ![]() �ص���
�ص���![]() Ϊֱ����Բ����ԭ��?�����ڣ�д��ֱ�ߵķ��̣��������ڣ�˵������.
Ϊֱ����Բ����ԭ��?�����ڣ�д��ֱ�ߵķ��̣��������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ĵ�����ֱ�����Σ�
�ĵ�����ֱ�����Σ�![]() ��
��![]() ��
��![]() ��
��![]() �������߳�Ϊ2���������Σ�
�������߳�Ϊ2���������Σ�![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() ���е�.
���е�.
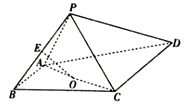
��1��֤����![]() ƽ��
ƽ��![]() .
.
��2�����߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹֱ��
��ʹֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() �������ڣ������
�������ڣ������![]() ��λ�ã��������ڣ�˵������.
��λ�ã��������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪��sinB+sinC����b��c������sinA+sinC��a��
��1����B��
��2����֪b��4����ABC�����Ϊ![]() �����ABC���ܳ���
�����ABC���ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com